0. 论文基本信息
题目:大跨桥梁阻尼伸臂减振研究
作者:陈林,刘展行,Satish Nagarajaiah, 孙利民*,赵林,崔巍

摘要:大跨桥梁结构频率低,阻尼小,易发生大幅振动(例如涡振),进而威胁桥梁结构的运营及安全。本文提出一种阻尼伸臂减振措施,通过控制主梁振动时的转角达到减振耗能的目的。建立了简化解析模型和有限元模型(以西堠门大桥为例),并考虑安装1个及多个阻尼伸臂的减振效果。结果表明阻尼伸臂可以同时对多模态提供较大的阻尼比,具有较好的减振性能。
论文链接:
https://doi.org/10.1016/j.engstruct.2022.114873
https://www.researchgate.net/publication/363582784
微信推送链接:
https://mp.weixin.qq.com/s/HUEYPXcsLsC9ZVAJXtGzeg
1. 研究背景
近年来,随着桥梁跨径的不断增加,桥梁柔度不断增加,已有多座大跨度悬索桥出现大幅涡振现象,包括中国的虎门大桥,西堠门大桥以及韩国的Jindo大桥等。现如今,大跨桥梁的风振控制主要包括气动措施和机械措施。气动措施主要通过改变桥梁断面结构的外形,破坏风场达到控制风振的效果。机械措施则一般通过控制桥梁结构的位移实现减振耗能的目的。机械措施中又包括直接耗能阻尼器和调谐质量阻尼器(TMD)。TMD可以针对结构安装位置处的绝对位移进行控制,故而有较广泛的应用场景。但是,TMD存在控制模态单一、质量块行程预留空间要求较大以及增加桥梁荷载等诸多问题。直接耗能阻尼器需要安装在结构两个相对位移较大的位置之间,安装位置受限。因此,大跨桥梁结构的减振仍是一个亟需解决的问题。近年来,有学者也提出了创新的阻尼减振措施。湖南大学陈政清院士和华旭刚教授团队[1][2]提出了在大跨悬索桥塔-梁间安装竖向阻尼器的措施,并验证该措施能够提升悬索桥多模态阻尼。
阻尼伸臂的概念首先在高层建筑减振体系中提出。连接高层建筑结构核心筒和框架柱并设置阻尼器,利用高层结构横向振动时核心筒与框架柱之间的相对位移进行振动控制。阻尼伸臂已经在高层结构中有诸多应用,并取得较好的效果。本研究受此启发,提出了针对主梁转角控制的桥梁阻尼伸臂措施。并通过简化解析模型和有限元模型对该措施的控制效果进行验证。
2. 桥梁阻尼伸臂概念
根据研究,在发生涡振时,桥梁的主梁在靠近桥塔的位置处转角较大。基于此,提出了一种针对大跨桥梁主梁转角控制的桥梁阻尼伸臂,如图1所所示。其中,竖向刚性伸臂一端安装在主梁上,其另一端连接水平阻尼器。当主梁发生振动时,刚性伸臂将主梁转角的角位移转化为伸臂末端的水平线位移,再通过主塔和伸臂间连接的水平阻尼器变形耗散能量,达到减振耗能的目的。
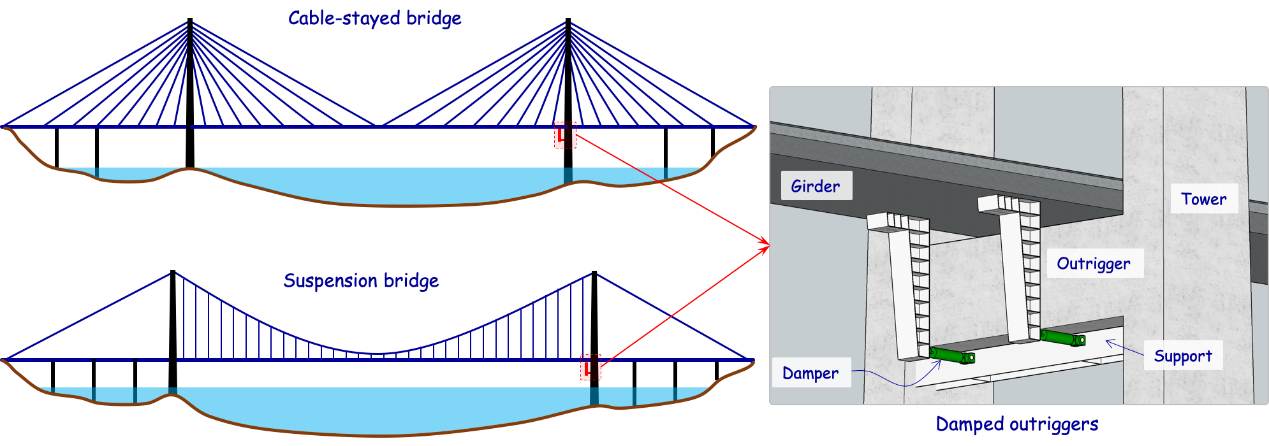
图1 桥梁阻尼伸臂概念
阻尼伸臂中的水平阻尼器沿桥梁纵向安装,当主梁在温度、车辆荷载等因素作用下出现纵向变形时,该阻尼器能够适应主梁纵向运动。同时,阻尼伸臂可以适用多种塔梁边界条件,包括飘浮体系和非漂浮体系,为桥梁多模态振动提供阻尼。然而,阻尼伸臂需要伸臂的刚度较大,以满足将主梁的转角传递到底部的阻尼器位置,需要阻尼器的行程也较大。本研究针对阻尼伸臂措施进行了初步的探索和尝试,具体实现效果和设计还需要后续进一步的分析。
3. 悬索桥简化模型
为了进一步研究阻尼伸臂对大跨度桥梁(以悬索桥为例)提供的阻尼效果,提出简化的张拉梁模型,进行初步的研究和分析。
3.1 张拉梁模型
如图2所示,将具有一个主跨和边跨的悬索桥结构简化为张拉梁模型。其中,将主梁和主缆的单位长度质量之和对应张拉梁的单位质量m,主缆中张力的水平分量以张拉梁中的水平张力H表示,主梁中的抗弯刚度则通过张拉梁的抗弯刚度EI模拟。张拉梁的总长度L为桥梁主跨和边跨的而总长度,l0代表阻尼伸臂安装位置距梁左端的距离。悬索桥上的阻尼伸臂的作用可以通过阻尼力矩Moi模拟。
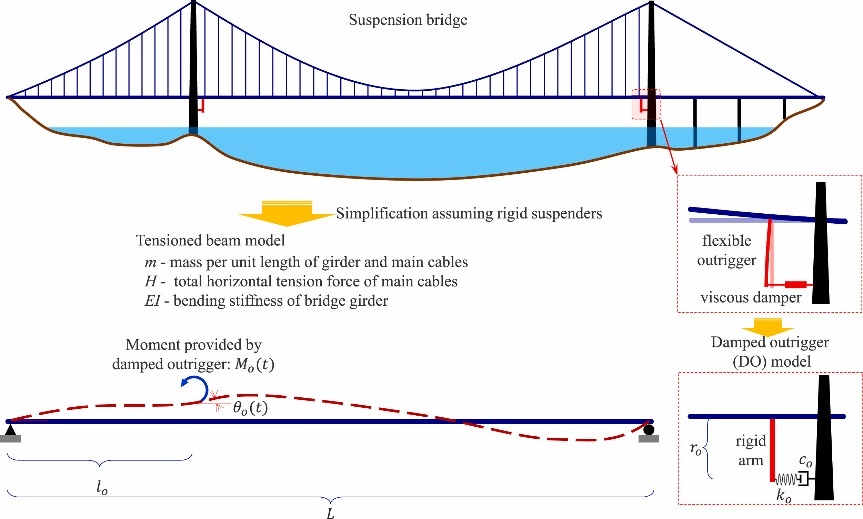
图2 桥梁阻尼伸臂概念
3.2 阻尼效果分析
张拉梁模型中的相对刚度γ代表结构的轴向刚度与抗弯刚度之比,其值定义为。由于相对刚度对阻尼伸臂的阻尼效果有非常重要的影响。因此,首先对典型悬索桥的相对刚度取值进行评估,几座典型悬索桥结构的相对刚度如表1所示。
表1 典型悬索桥的结构参数
| 悬索桥 | 主跨长度(m) | 边跨长度(m) | 总长度(m) | 相对刚度 |
1 | 西堠门大桥 | 1650 | 578 | 2228 | 77.14 |
2 | 润扬长江大桥 | 1490 | —— | 1490 | 37.35 |
3 | The Great Belt Bridge | 1624 | 535×2 | 2694 | 63.56 |
4 | 江阴长江大桥 | 1385 | —— | 1385 | 71.32 |
5 | The Faith Sultan Mehamet Bridge | 1090 | —— | 1090 | 34.81 |
6 | 杨泗港大桥 | 1700 | —— | 1700 | 74.71 |
可以看出对于大多数悬索桥,相对刚度γ的范围在30-80之间。在后续分析中,主要采用γ=50作为一般情况。
由于大跨桥梁结构的涡振通常表现为多模态振动,因此考虑了张拉梁模型的前8阶竖弯振动。安装单个阻尼伸臂时,假定安装在张拉梁模型最左端,伸臂为刚性,此时前8阶频率、阻尼系数与阻尼比的关系如图3所示。
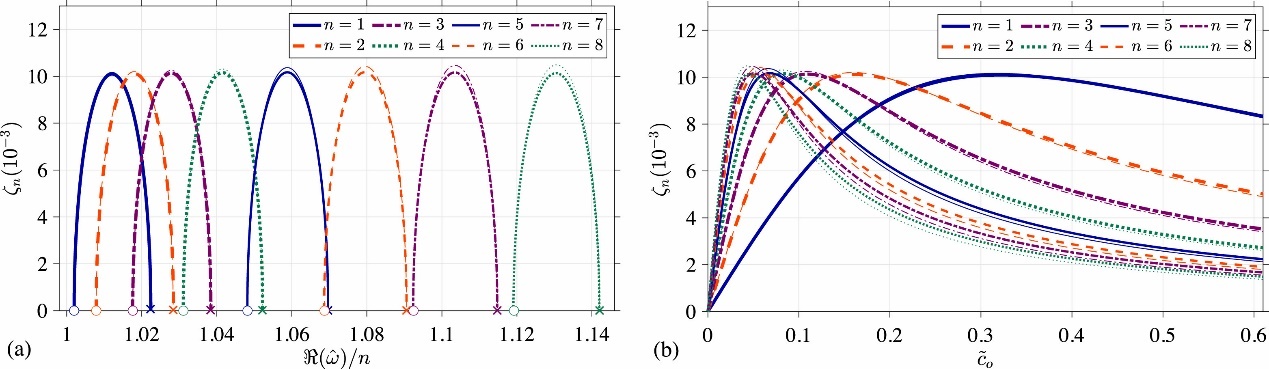
图3 安装单个阻尼伸臂时前8阶阻尼比: (a) 随阻尼系数增加,频率与阻尼比轨迹; (b) 阻尼曲线。
此时,单模态最大阻尼比约为1.0%,基本满足桥梁涡振控制要求。但是,当考虑多模态控制时(无量纲化最优阻尼系数取值)此时前8阶模态阻尼比仅能保证均大于0.6%。
4. 有限元模型分析
4.1 桥梁实例
为进一步验证阻尼效果,本研究针对位移浙江省舟山市的西堠门大桥进行建模,并分析了安装阻尼伸臂对悬索桥的影响。西堠门大桥是一座分离式双箱梁悬索桥。其主跨1650 m,边跨578 m(北侧)。根据桥梁健康监测数据显示,该桥多阶模态在运营过程中出现涡振。因此,以该桥为研究目标具有一定的实际意义。
该桥的有限元模型如图4所示。其中,该桥分别有三个可能安装阻尼伸臂的位置,分别在北桥塔处、南桥塔处和北锚固点位置,分别记作位置1、2和3。由于主梁结构为分离式钢箱梁,因此阻尼伸臂也在两条钢箱梁下方两侧各安装一半结构。单侧阻尼伸臂的阻尼系数为计算的总阻尼系数的一半。伸臂的高度取值15 m,伸臂与塔/锚固点之间的水平距离取决于最近的横梁位置。在本研究中,由于阻尼伸臂本身能够起到抑制主梁纵向运动的效果,因此不再设置原结构中存在的纵向阻尼器。
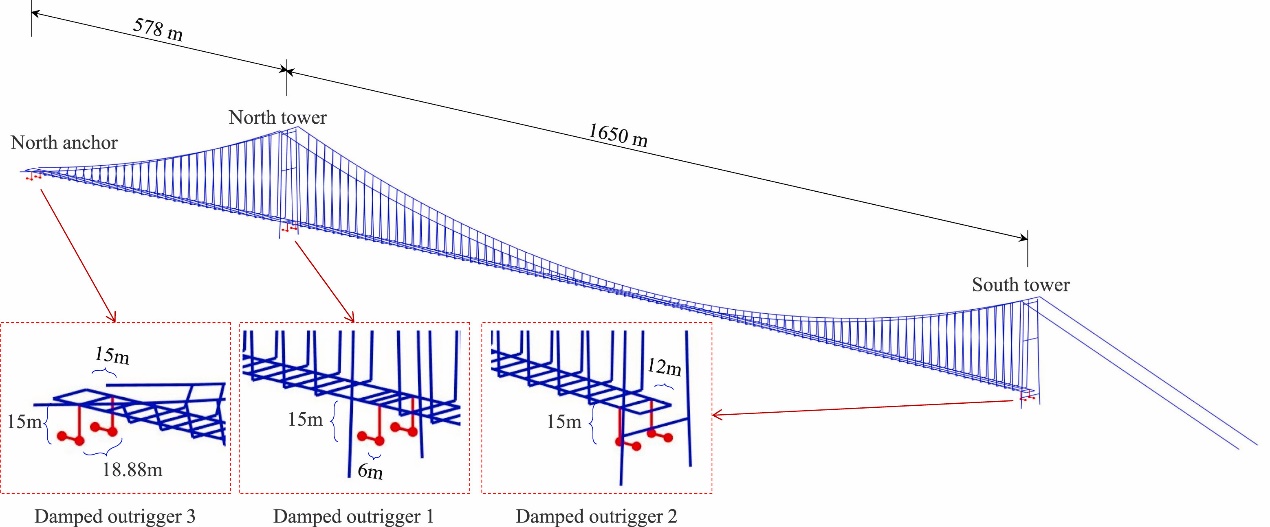
图4 西堠门大桥有限元模型
西堠门大桥有限元模型计算前15阶竖弯振型及主梁转角如图5所示。
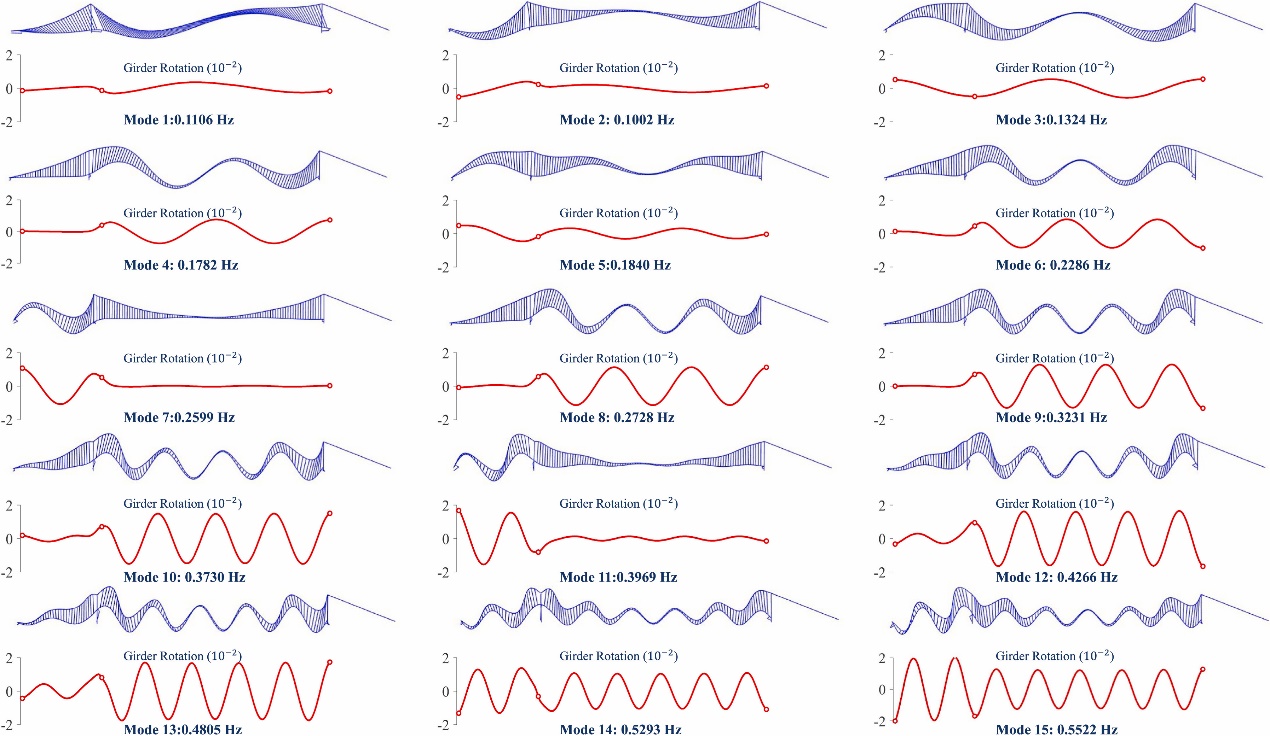
图5 西堠门大桥有限元模型前15阶竖弯模态振型
根据监测信息可知,在西堠门前14阶竖弯振型中,主要有7阶模态发生过显著涡振,分别为第5、6、8、9、10、12和13阶竖弯模态。
4.2 阻尼伸臂提供的阻尼效果
在主梁不同位置安装阻尼伸臂时,由于主梁转角、振型的不同,阻尼伸臂能提供的最大阻尼比也有一定的差异。位置1,2处的阻尼伸臂主要针对主跨振动有较好的控制作用,而位置3处的阻尼伸臂仅针对边跨振动效果明显。考虑安装单个阻尼伸臂时,优选安装在位置2处;安装多个阻尼伸臂时,应当首先保证对主梁主跨振动的减振效果。
(1)阻尼伸臂安装在位置2
安装单个阻尼伸臂在位置2处时,阻尼伸臂能提供最优减振效果。此时,桥梁前14阶竖弯模态阻尼曲线绘制在图6中。
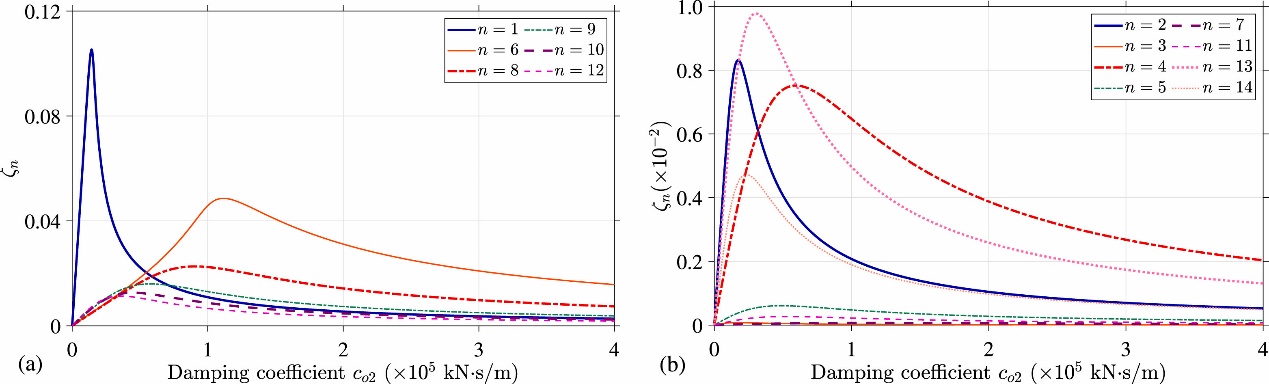
图6 阻尼伸臂安装在位置2处时阻尼曲线。
对于第3、5、7和11阶振型,阻尼伸臂提供的阻尼比较小(小于0.1%)。对于发生涡振的模态,除第5阶由于阻尼伸臂安装位置的主梁转角较小,阻尼伸臂提供的阻尼比较小外,其他6阶模态,阻尼伸臂均能提供约1.0%及以上的阻尼比,与简化模型计算结果相近。
(2)阻尼伸臂安装在位置1和2
当考虑安装两个阻尼伸臂时,优选安装在位置1和2处。此时,取两处的阻尼伸臂的阻尼系数相等,即co1=co2。阻尼曲线如图7所示。
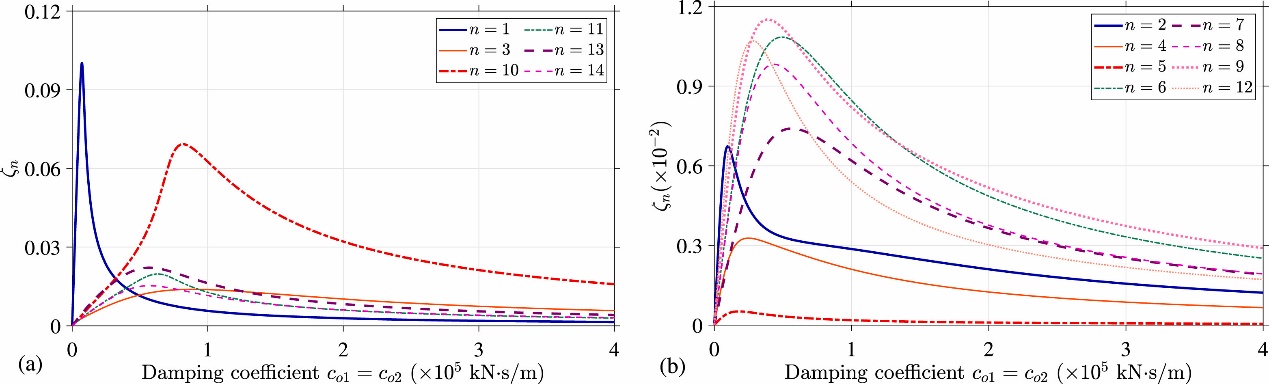
图7 阻尼伸臂安装在位置1和2处时阻尼曲线()。
安装2个阻尼伸臂后,一些模态的最大阻尼比有所增加,第3阶和第14阶模态最大阻尼比增加至1.0%以上。同时,也有一些模态的最大阻尼比反而有所下降,第8阶和第9阶模态的最大阻尼比小于安装单个阻尼伸臂的情况。
因此,单纯的增加阻尼伸臂的个数并不一定能够提高阻尼伸臂的减振效果,阻尼伸臂参数的优化还需要进一步的研究。
(3)阻尼伸臂参数设计
安装一个阻尼伸臂时,优选应该安装在南塔(位置2)处。此时,最优阻尼系数的选取考虑第8和12阶竖弯模态下阻尼曲线的交点,即co2=0.32x105kN·s/m。此时,在前14阶竖弯模态中,有9阶模态阻尼比大于0.5%,有7阶模态阻尼比大于1.0%。在发生涡振的7阶模态中,有6阶模态的阻尼比达到1.0%及以上。
安装两个阻尼伸臂时,两处阻尼系数取值相等。此时最优阻尼系数通过第6阶和第12阶竖弯模态阻尼曲线交点确定,即co1=co2=0.36x105kN·s/m。安装2个阻尼伸臂后,在前14阶竖弯模态中,有11阶模态阻尼比达到0.5%以上,其中8阶模态阻尼比在1.0%以上。结果如表2所示。
表2 阻尼伸臂对多模态减振效果
模态阶次 | 是否涡振[3][4] | 频率 (Hz) | 结构阻尼比(%)[3][4] | 附加阻尼比(%) |
单个阻尼伸臂(2) | 两个阻尼伸臂(1&2) |
1 | —— | 0.0934 | 0.57 | 3.65 | 1.60 |
2 | —— | 0.1002 | —— | 0.61 | 0.37 |
3 | —— | 0.1324 | 0.52 | 0.01 | 0.96 |
4 | —— | 0.1782 | —— | 0.61 | 0.31 |
5 | 是 | 0.1840 | 0.50 | 0.06 | 0.04 |
6 | 是 | 0.2286 | 0.51 | 1.13 | 1.03 |
7 | —— | 0.2599 | —— | 0.00 | 0.66 |
8 | 是 | 0.2728 | 0.39 | 1.08 | 0.96 |
9 | 是 | 0.3231 | 0.42 | 1.27 | 1.15 |
10 | 是 | 0.3731 | —— | 1.17 | 2.04 |
11 | —— | 0.3969 | —— | 0.02 | 1.32 |
12 | 是 | 0.4266 | 0.37 | 1.12 | 1.03 |
13 | 是 | 0.4805 | 0.32 | 0.98 | 1.85 |
14 | —— | 0.5293 | —— | 0.44 | 1.26 |
5. 结论
本研究初步尝试了安装阻尼伸臂对大跨悬索桥结构多模态阻尼的效果,以西堠门大桥为例,采用了简化解析模型和有限元模型分析,得到以下结论:
阻尼伸臂可以有效对大跨桥梁多阶模态提供附加阻尼;
对于西堠门大桥,安装一个阻尼伸臂时,优选安装在南塔(位置2)处,对多阶模态控制效果最佳。前14阶竖弯模态中,有7阶模态最大阻尼比可以达到0.98%及以上;安装两个阻尼伸臂在北塔(位置1)和南塔(位置2)时,前14阶模态中有8阶模态最大阻尼比达到1.0%以上,多模态阻尼提升效果较好;
某些竖弯模态中出现耦合纵飘振型,可能造成阻尼器的行程较大,在实际工程应用时需要进一步的分析;
安装多个阻尼伸臂时,某些模态阻尼比反而会出现下降,因此不同位置阻尼系数的选取仍需要进一步的优化。
6. 参考文献
[1] 华旭刚,黄智文,陈政清.大跨度悬索桥的多阶模态竖向涡振与控制[J].中国公路学报,2019,32(10):115-124.
[2] 陈政清,华旭刚,牛华伟,黄智文,张弘毅,陈谨林.永磁电涡流阻尼新技术及其在土木工程中的应用[J].中国公路学报,2020,33(11):83-100.
[3] Li H, Laima S, Ou J, et al. Investigation of vortex-induced vibration of a suspension bridge with two separated steel box girders based on field measurements[J]. Engineering Structures, 2011, 33(6): 1894-1907.
[4] Li H, Laima S, Zhang Q, et al. Field monitoring and validation of vortex-induced vibrations of a long-span suspension bridge[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2014, 124: 54-67.