0. 论文基本信息
题目:基于物理导引卷积神经网络的桥梁车致位移响应重构
摘要:挠度是评估桥梁运营状态的重要指标,但是由于通常需要一个固定的参考点而导致很难直接测量。本文提出了一种间接测量历史位移响应数据的方法,应用卷积神经网络(CNN)来近似桥梁响应之间的映射关系,从而通过其他种类的响应重构所需挠度数据。本文采用了物理导引的深度学习理念,利用桥梁车致位移重构问题相关的先验知识指导网络结构的设计。所提出的网络模型具有两个独立分支,分别估计准静态位移成分和动态位移成分。在这之后,将二者在后接主干中融合修饰从而得到最终结果。除此之外,损失函数中包括了基于物理设计的额外的正则项,即位移和加速度之间的计算关系。此物理损失可以帮助指引网络训练方向,减轻过拟合问题,且改进算法在高频响应重构上的性能。本文通过两个数值模拟示例和一个实验室模型试验验证了方法的性能和可应用性。
论文链接:
https://www.sciencedirect.com/science/article/abs/pii/S0045794922001237
https://www.researchgate.net/publication/362148786_Traffic-induced_bridge_displacement_reconstruction_using_a_physics-informed_convolutional_neural_network
引用格式:
Ni, P., Li, Y., Sun, L., & Wang, A. Traffic-induced bridge displacement reconstruction using a physics-informed convolutional neural network. Computers & Structures. 2022; 271: 106863. https://doi.org/10.1016/j.compstruc.2022.106863
微信推送链接:
https://mp.weixin.qq.com/s/Vd4WNtY0FSsPgO1EnJpzvA
1. 研究背景
近年来,结构健康监测(SHM)技术已被广泛应用于基础设施维护中。数据是结构健康监测的重要基础,而其中,位移响应数据又在诸多研究和应用中起着重要的作用。目前可以高精度直接测量结构位移响应的手段,通常需要依赖一个固定的参考点,这有时是很昂贵甚至无法实现的。除此之外,一些仪器设备本身就很昂贵,限制了其应用。
为了克服直接测量手段的局限,旨在将其他种类的测量数据融合转换为所需要的位移响应数据的间接方法被广泛研究。在这些方法中,加速度和应变常被应用。加速度响应便于测量,可以通过时域积分得到位移,但是通常有因低频噪声引起的漂移问题[1,2]。同时,仅靠加速度数据很难获取准静态位移成分。另一方面,基于应变的位移重构方法虽然不会有这些问题,但容易收到高频噪声的影响,同时需要确定的中性轴位置。在这种情况下,有学者,如Park 等[3],创新地将加速度和应变融合,应用应变模态叠加来帮助预防信号漂移问题。
深度学习方法,以其强大的非线性拟合能力,在很多领域都吸引了广泛的关注。在结构响应重构领域内自然也如此。多种结构样式的深度神经网络(DNN)被设计提出用于响应重构,但这些方法中,大量的数据集往往是必需的。鉴于收集大量高质量数据需要很多时间精力,在小数据集下训练网络模型并获得鲁棒的结果是很有意义的。物理导引的深度学习(Physics-informed Deep learning)是近来新兴的概念。其旨在将先验知识或物理法则融入到神经网络模型中,以约束并引导网络学习过程,帮助减缓小训练数据集时易出现的过拟合问题,提高网络的性能。本文提出了一种物理导引的卷积神经网络,服务于桥梁车致位移响应的重构。
2.研究方法
2.1 卷积和逆卷积
所提出网络基本由卷积曾和逆卷积层组成。卷积层在输入上实施卷积操作以提取特征,如图。卷积过程(如图1)可以通过如下公式描述:
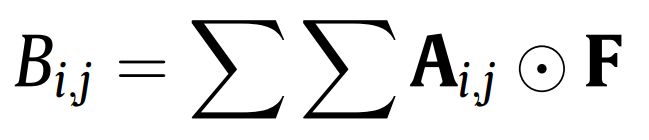
其中,B代表合成矩阵B的元素,Ai,j是输入的子阵列,F代表滤波器,⊙代表按元素乘积。逆卷积,又称转置卷积,通常用于上采样,其操作过程如图2所示。
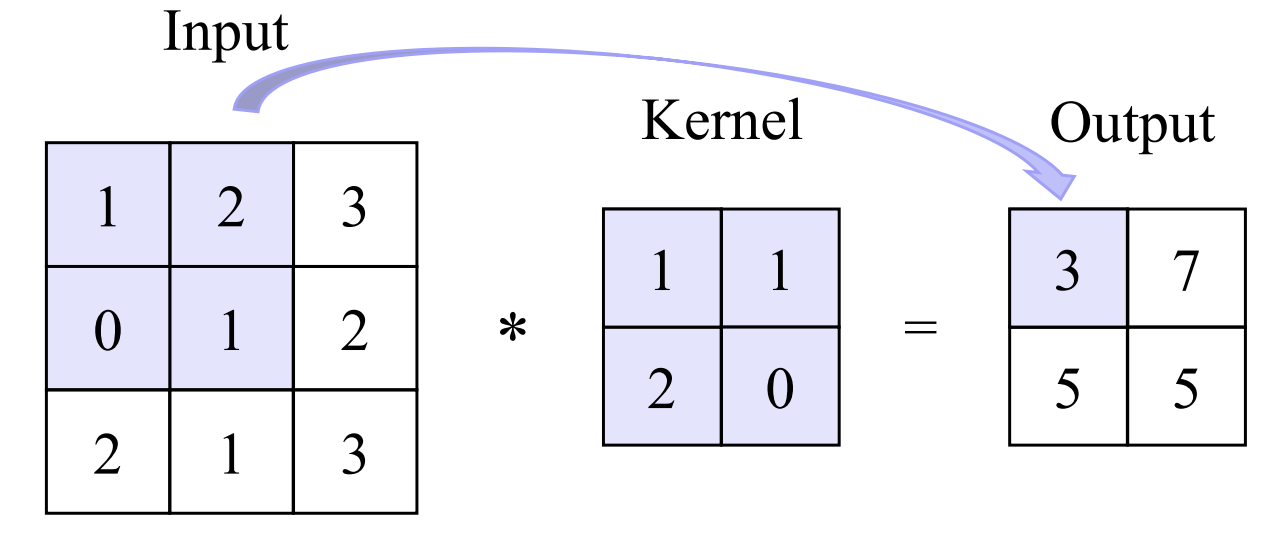
图1 卷积运算示意图
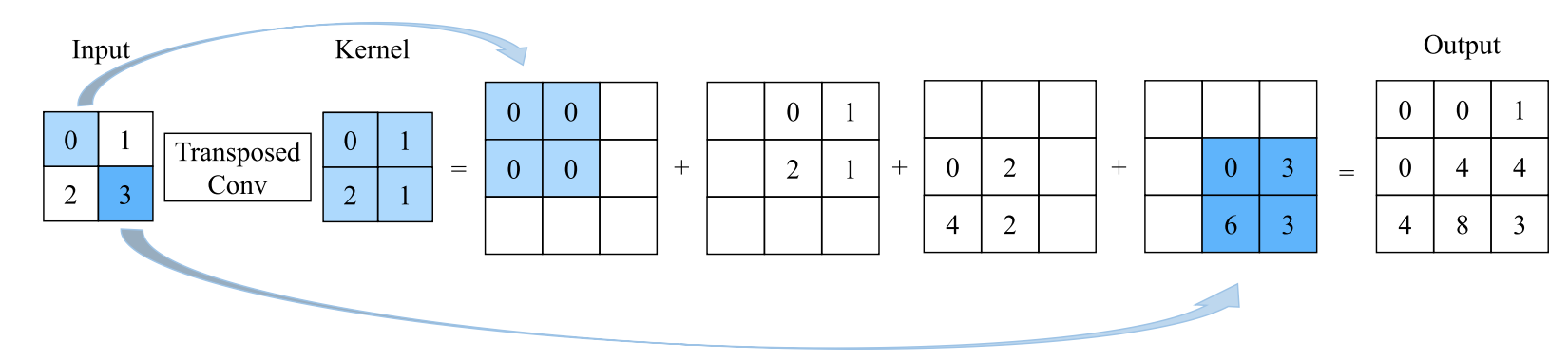
图2 逆卷积运算示意图
2.2 残差编码器-解码器模块
本研究中采用了自编码器(编码-解码)结构,其包括两部分,即编码器和解码器。编码器部分由多个带有下采样功能的卷积层组成,从输入逐渐提取高维特征。解码器部分则借助逆卷积层逐渐上采样重构至输出目标。此外,自编码器和残差结构结合,得到残差编码器-解码器模块结构(Residual Encoder-Decoder),其结构具体如图3所示。
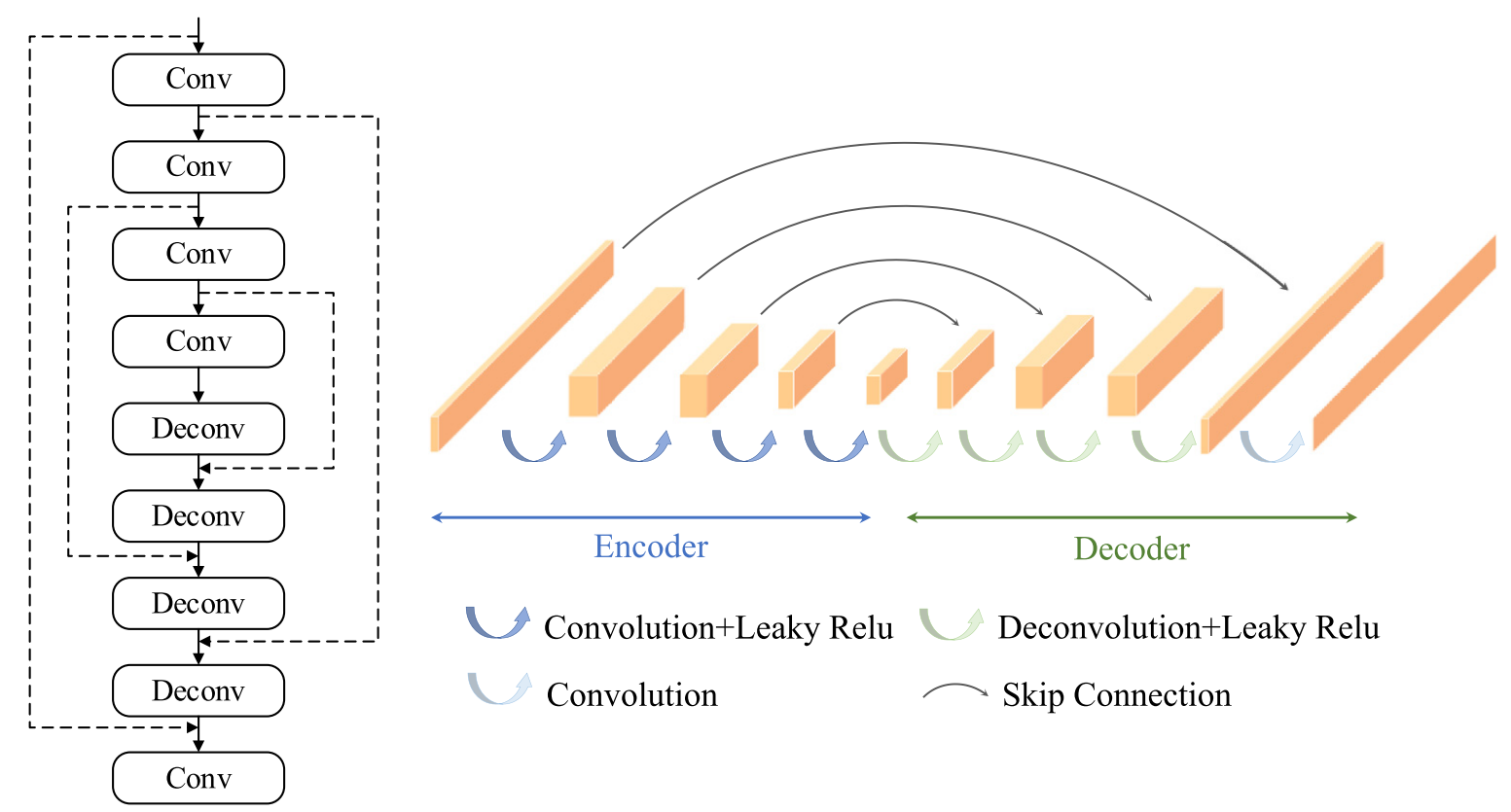
图3 残差编码器-解码器模块结构
2.3 物理导引深度神经网络结构
本文所提出网络结构如图4所示。网络结构基于已有物理先验信息设计,能够对不同种输入响应实现有目的、有计划地应用。网络包含两个分支,以输入应变和加速度响应为例,网络首先通过应变和加速度分别重构准静态位移成分和动态位移成分,之后再将二者融合并进一步修饰以获得整体位移响应。所设计网络结构不包含任何池化层。网络不同分支结构相似,都由单独卷积层和残差编码器-解码器结构组成,整体上结构工整,便于应用或修改。网络各层超参基本布置总结于表1。
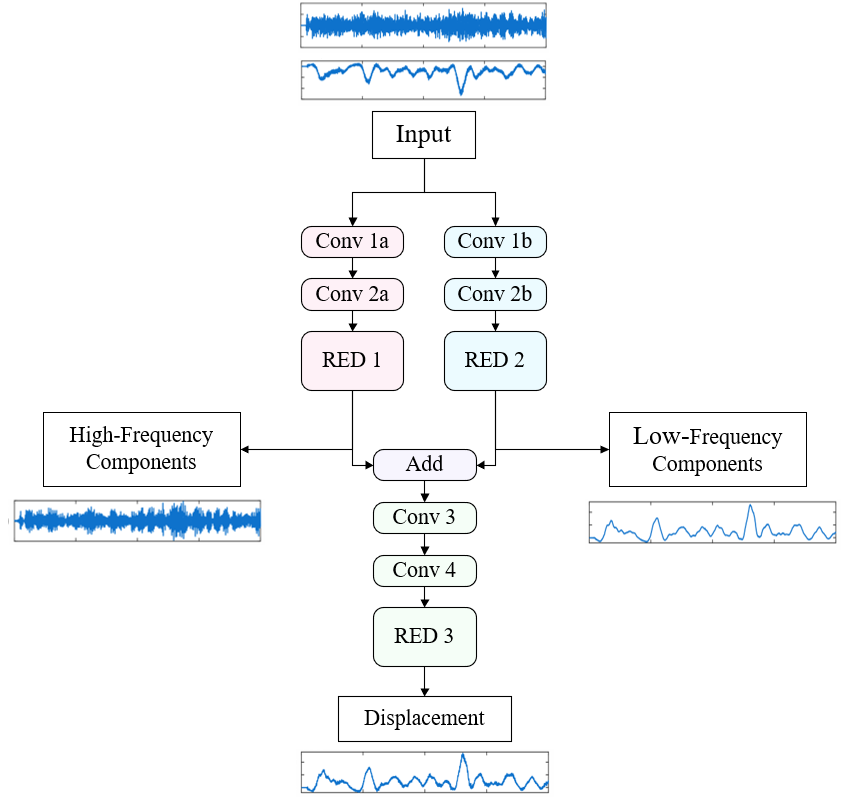
图4 网络结构图
表1 网络基本配置
网络层 | 卷积核尺寸 | 步长 | 卷积核数 |
Conv 1a | 1×5 | 1×1 | 16 |
Conv 1b | 1×7 | 1×1 | 16 |
Conv 2a | 1×5 | 1×1 | 16 |
Conv 2b | 1×7 | 1×1 | 16 |
Conv 3 | 1×3 | 1×1 | 16 |
Conv 4 | 1×3 | 1×1 | 16 |
RED 1 | Convs: 1×5
Deconvs: 1×2 | 4@Convs: 1×2 +
4@Deconvs: 1×2
+
1@Convs: 1×1 | Convs: [64,64,32,32] +
Deconvs: [32,64,64,16]
+
Conv: [1] |
RED 2 | Convs: 1×5
Deconvs: 1×2 |
RED 3 | Convs: 1×3
Deconvs: 1×2 |
2.4 物理导引的损失函数设计
除基于物理先验知识的网络结构设计以外,网络训练的损失函数也借助物理导引而设计。损失函数由均方误差损失项(或称经验损失项)和物理损失项组成,如下式:
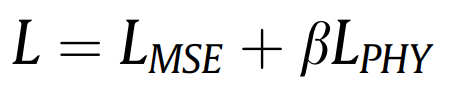
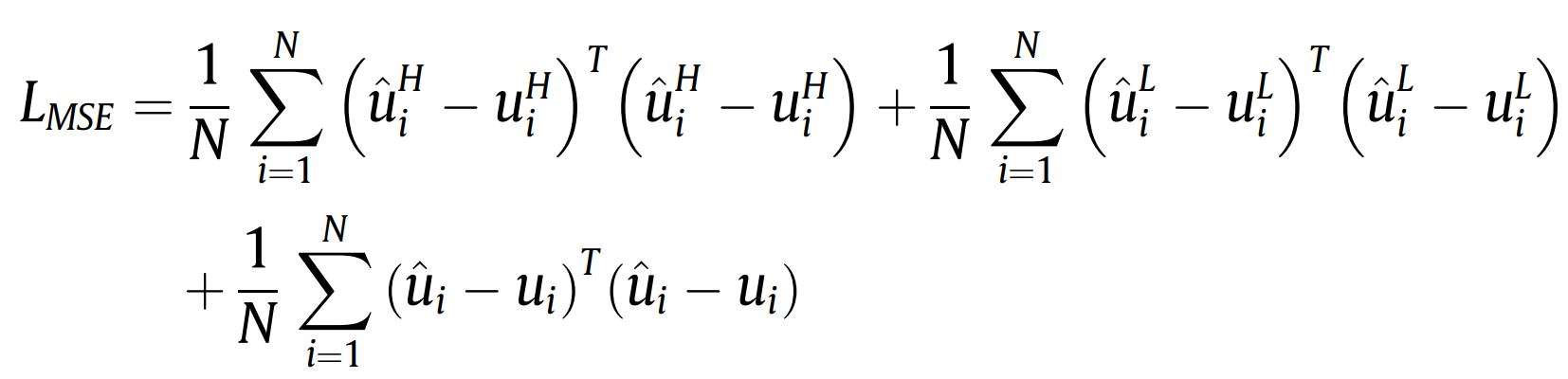
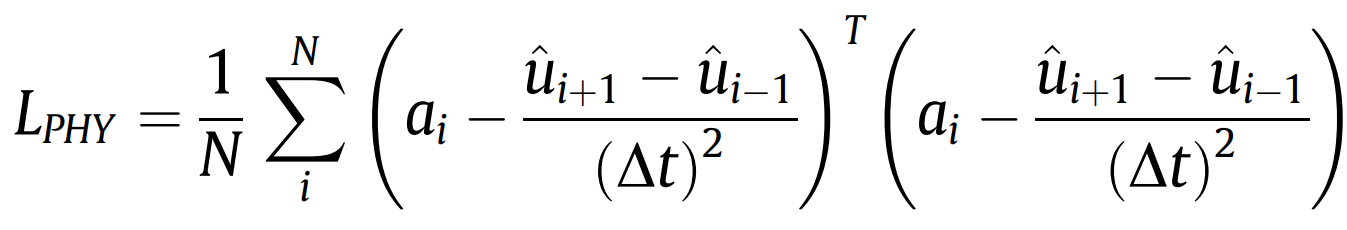
其中,L代表损失函数,LMSE代表经验损失项,LPHY代表物理损失(物理导引设计),β为一常数值,用于调节的权重占比。ui(带上标)和ui分别代表重构位移和测量位移。N代表数据长度。上标H和L分别代表高频(动态)和低频(准静态)成分。
2.5 数据准备和网络训练
因本文所提方法需要,监测的位移数据在应用到网络训练之前,需先通过高通滤波器特殊处理,分解为低频(准静态)成分和高频(动态)成分。本文采用基于有限脉冲响应(FIR)的方法设计所需的高通滤波器:
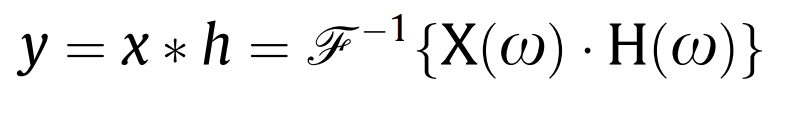
其中,x和y为输入和输出信号。X()和H()分别指输入信号和滤波器的频率幅值。
本文采用Adam优化算法训练网络。所提网络约有210,000个可训练参数。训练基本采用较小学习率,以使网络训练过程尽量平稳,防止迅速陷入局部最优。同时采用了早停策略以防止明显过拟合。
3. 数值验证
3.1 简支梁
本文应用一长20米的简支梁数值模型来验证方法可行性。模型梁被分为40个单元,总共具有120个自由度,其中只考虑平面内变形。梁1/4和1/2跨处分别安装了虚拟应变计、加速度计和位移计来收集训练数据。模型布置如图5所示。

图 5 桥梁模型和传感器布置
模拟交通流荷载被施加在模型桥上以计算桥梁响应。车辆简化为匀速运动的集中力,并忽略车桥相互作用。车辆荷载、速度、自振频率被假定服从以下有限范围内高斯分布:

对每一个车辆,其对桥梁作用可以表示为:

计算桥梁2.4×104 s内的响应用于网络训练。传感器采样频率为100HZ。网络输入为应变和加速度数据,输出位移响应。通过移动窗口法划分训练样本,总共得到9600个样本,其中20%样本用于验证集。
网络训练超参数设置如下:
表2 加速度传感器性能
超参数 | 值 |
学习率 | 5×10-5 |
Batch大小 | 64 |
训练迭代步 | 150 |
β | 1×10-8 |
输入规格 | 5,4000 |
网络训练过程如图6所示。
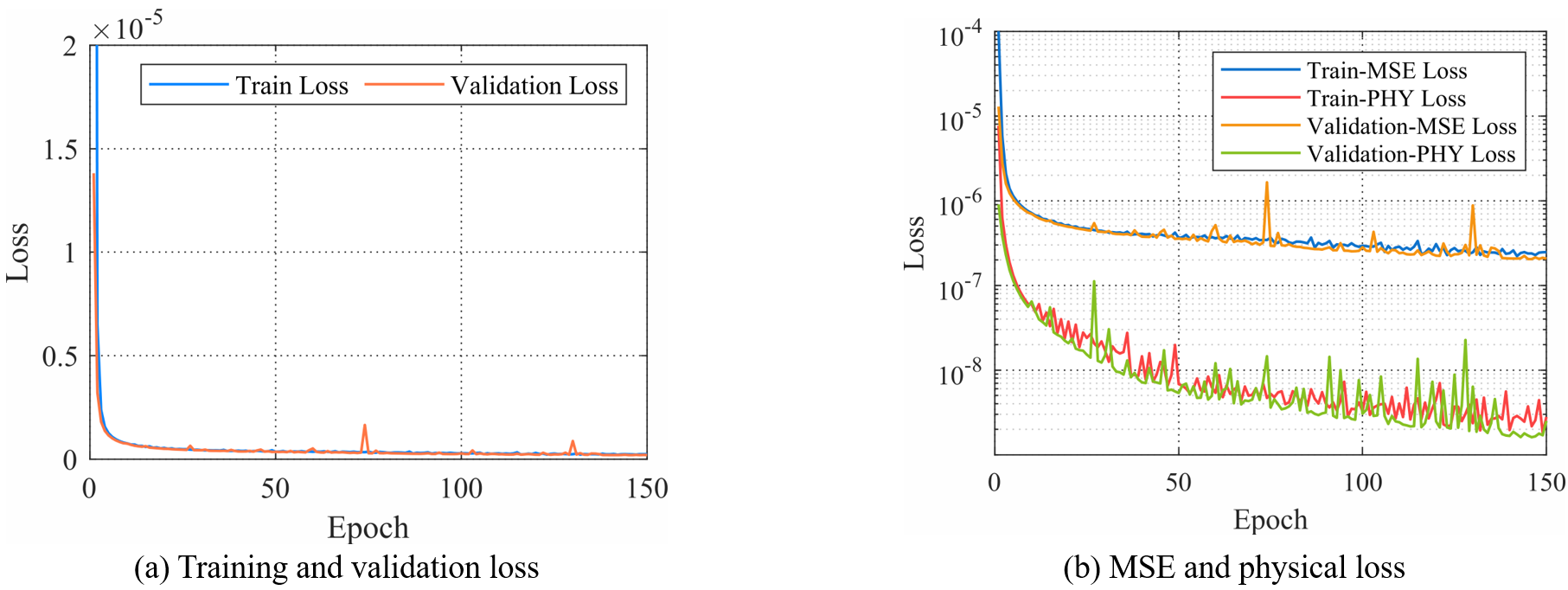
(a)训练和验证损失曲线 (b) MSE损失和物理损失占比
图6 损失曲线
网络重构1/2跨和1/4跨位移响应的结果如图7所示。尽管在一些极值位置处有一定误差,重构位移整体均和有限元模型计算真值较好符合。两处位移重构最大绝对误差分别为0.26cm和0.16cm,平均相对误差分别为1.12%和1.22%。
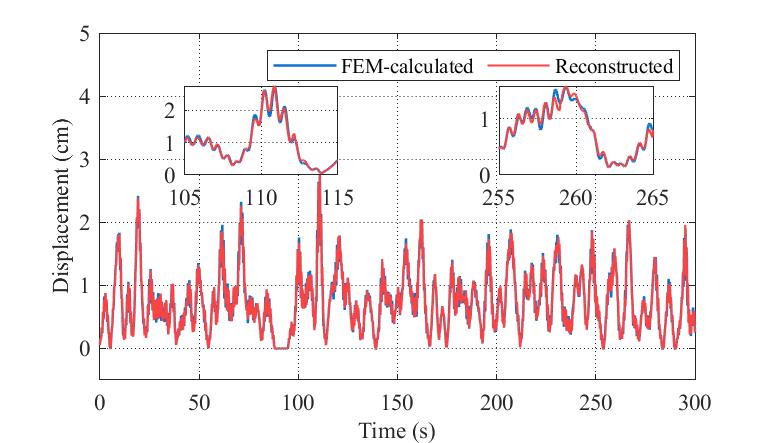
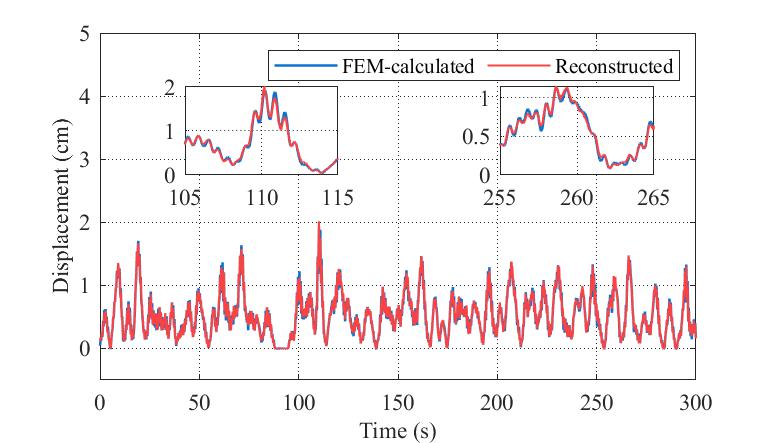
20号节点(跨中)位移重构 (b) 10号节点(1/4跨)位移重构
图7 位移重构结果
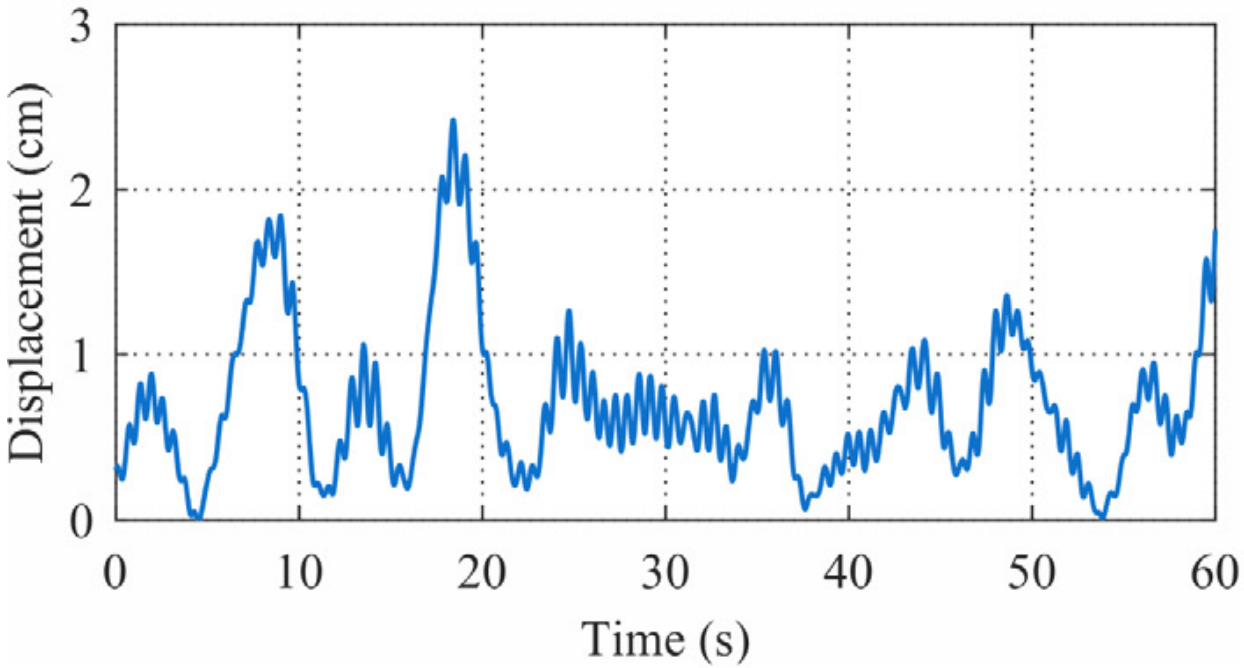
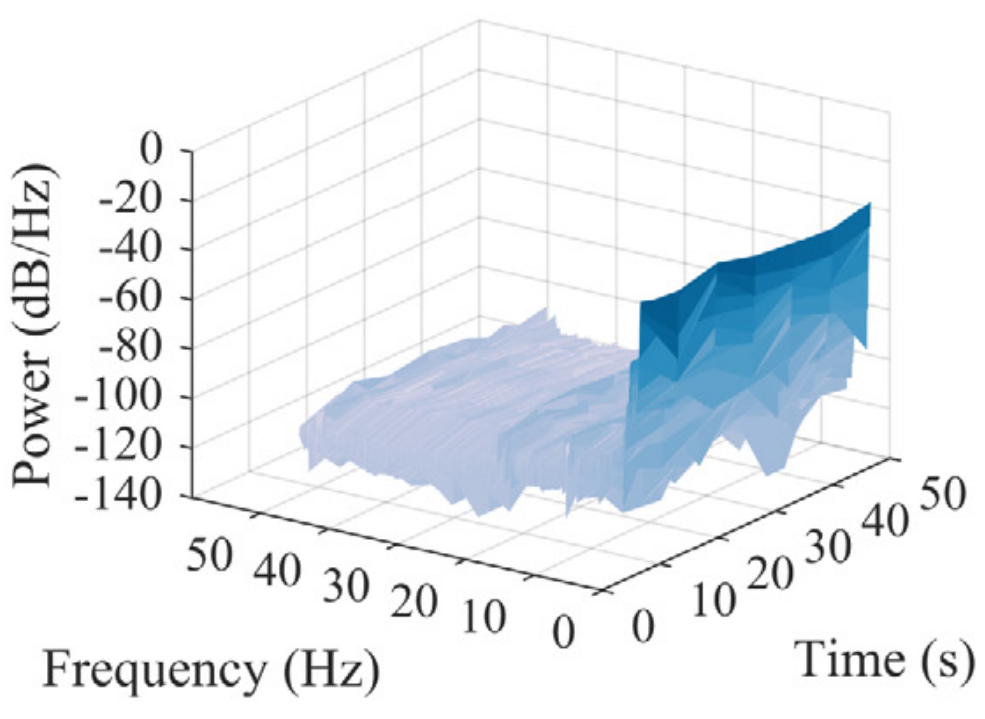
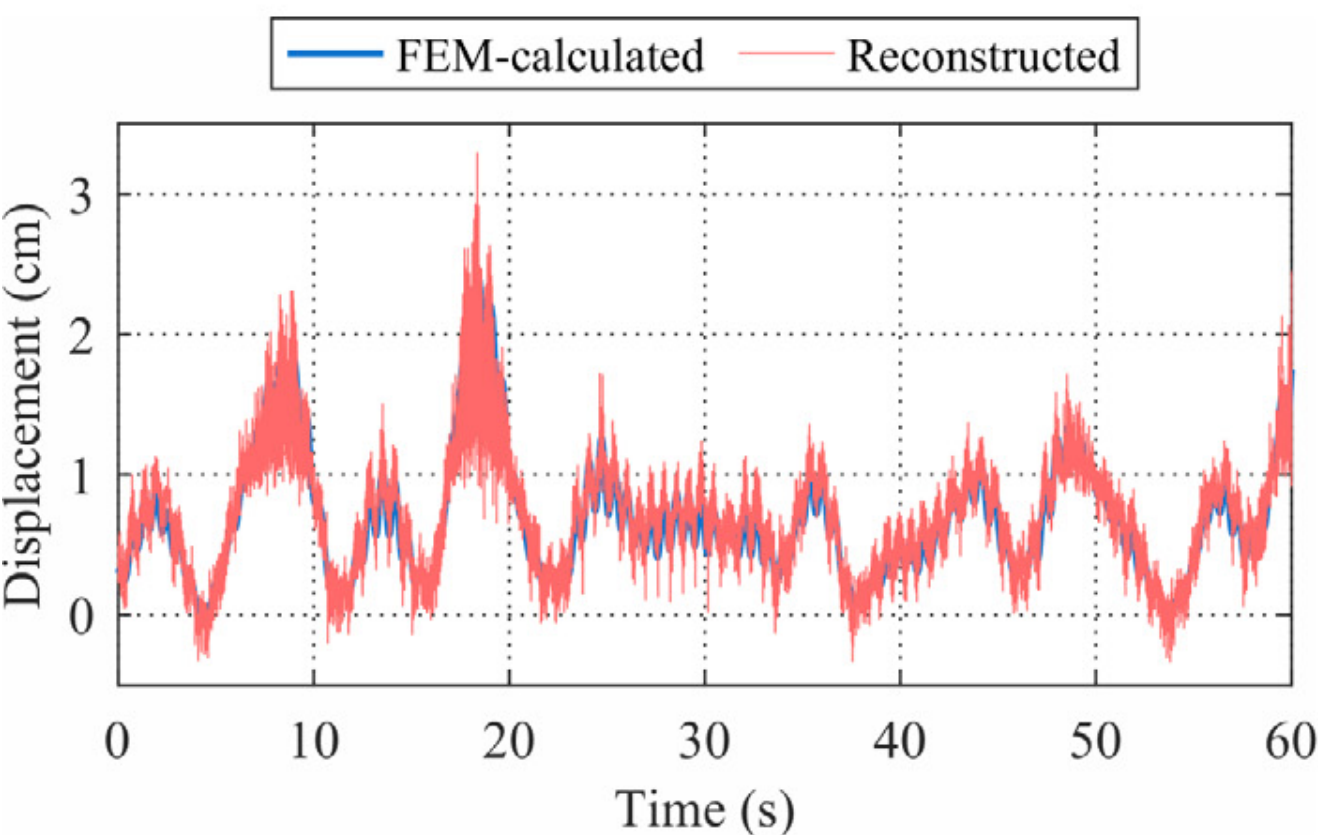
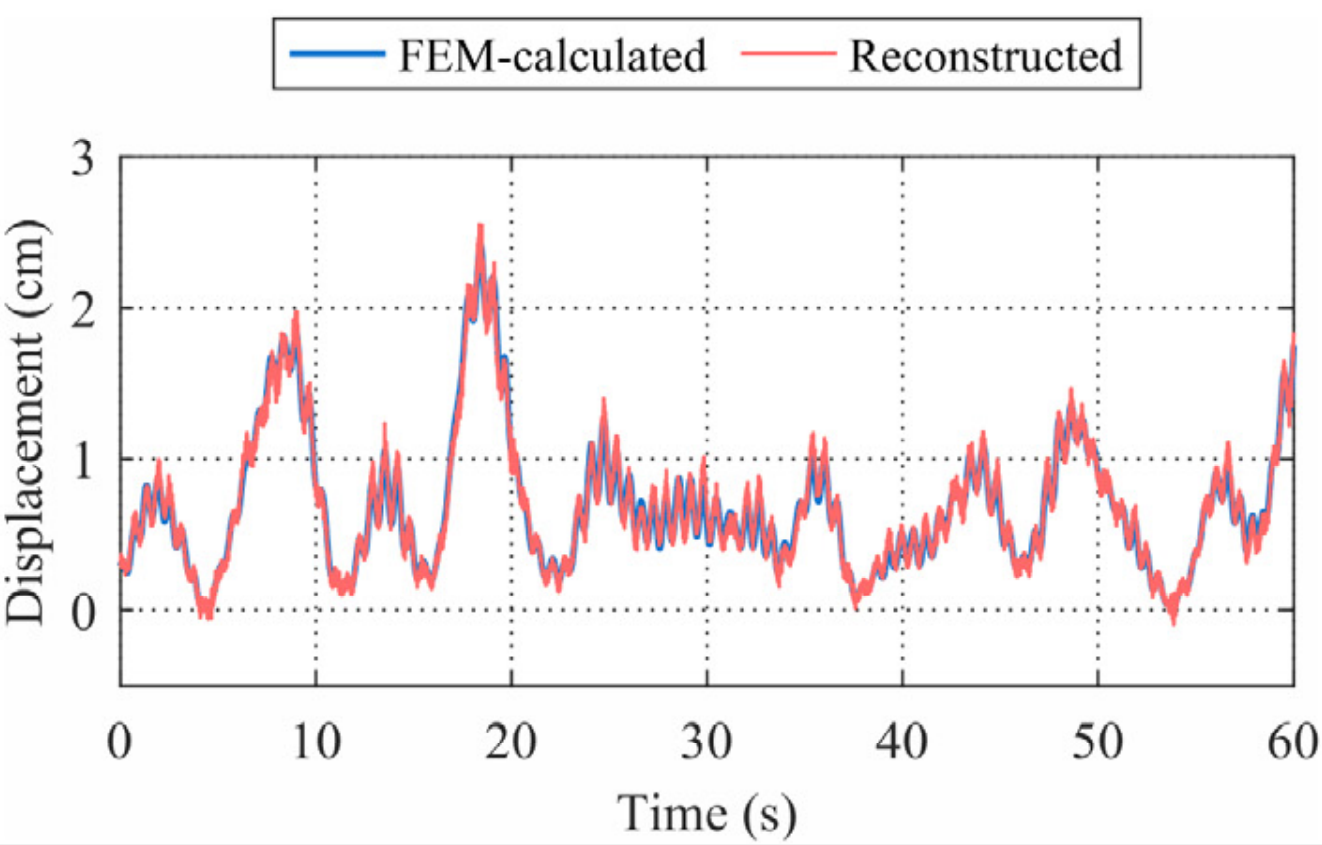
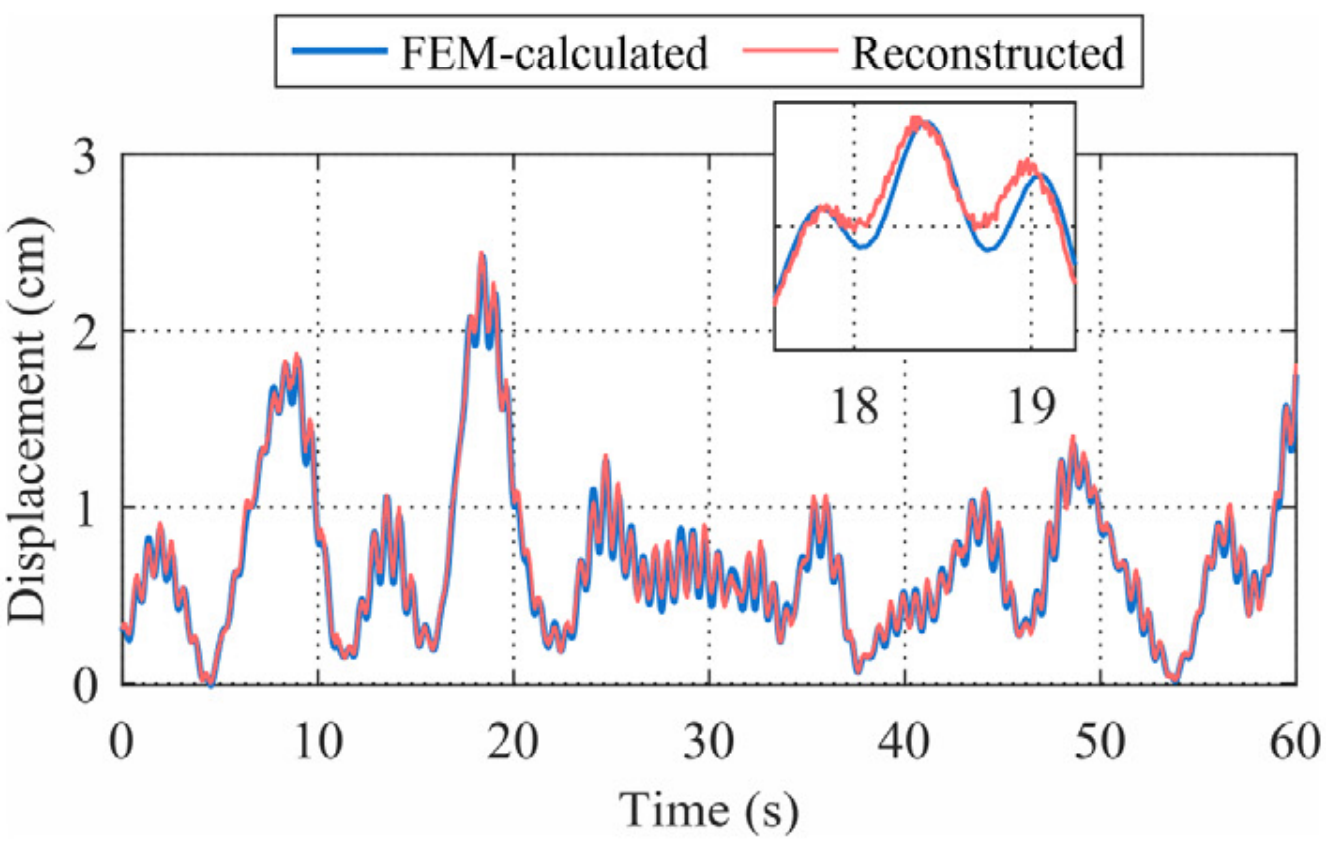
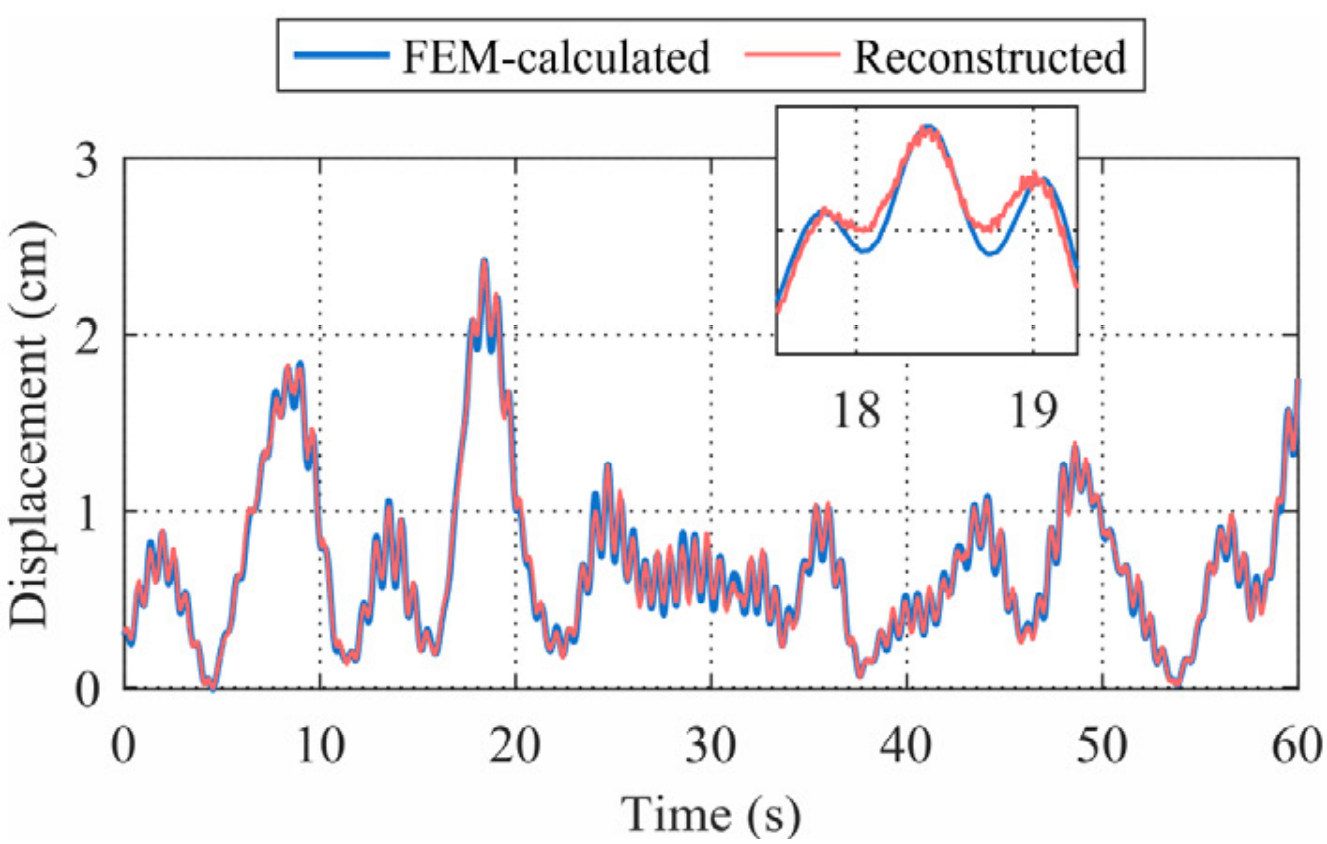
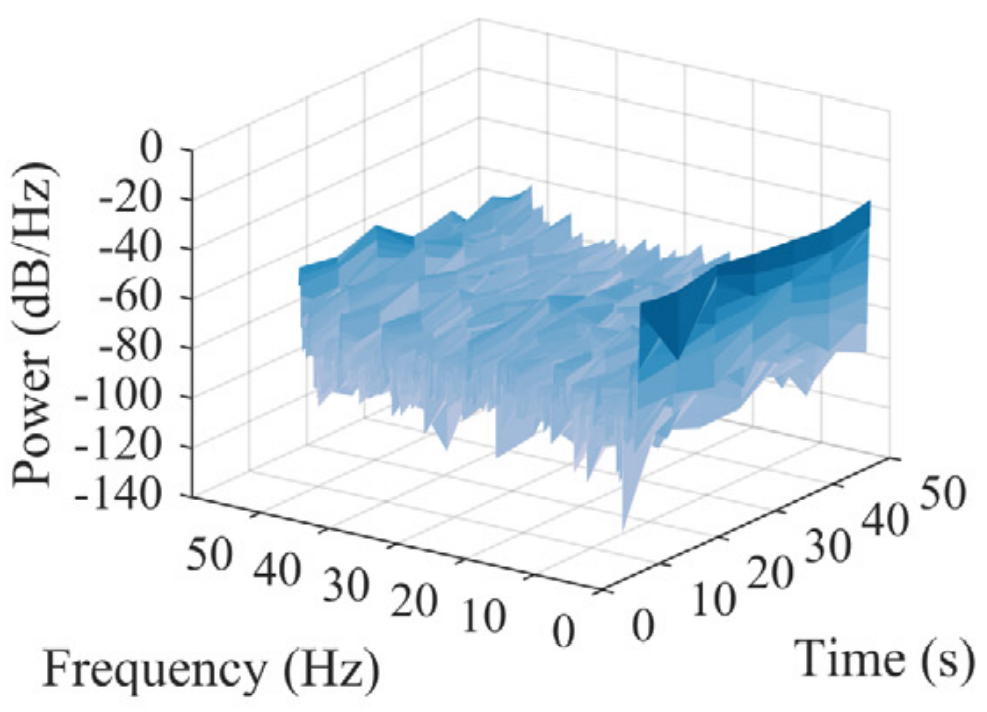
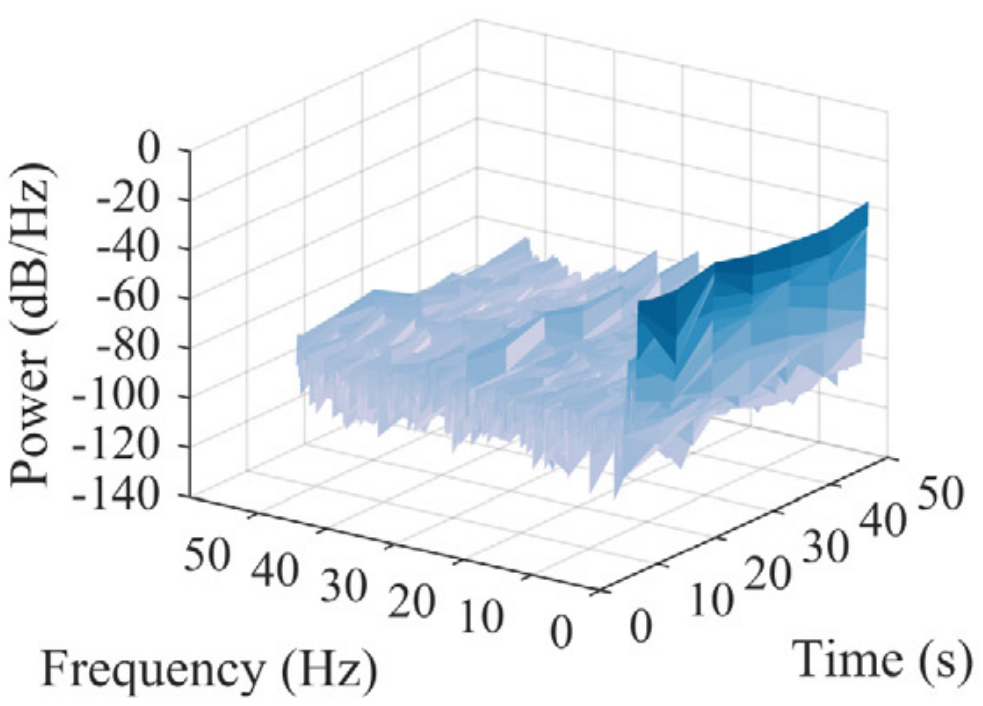
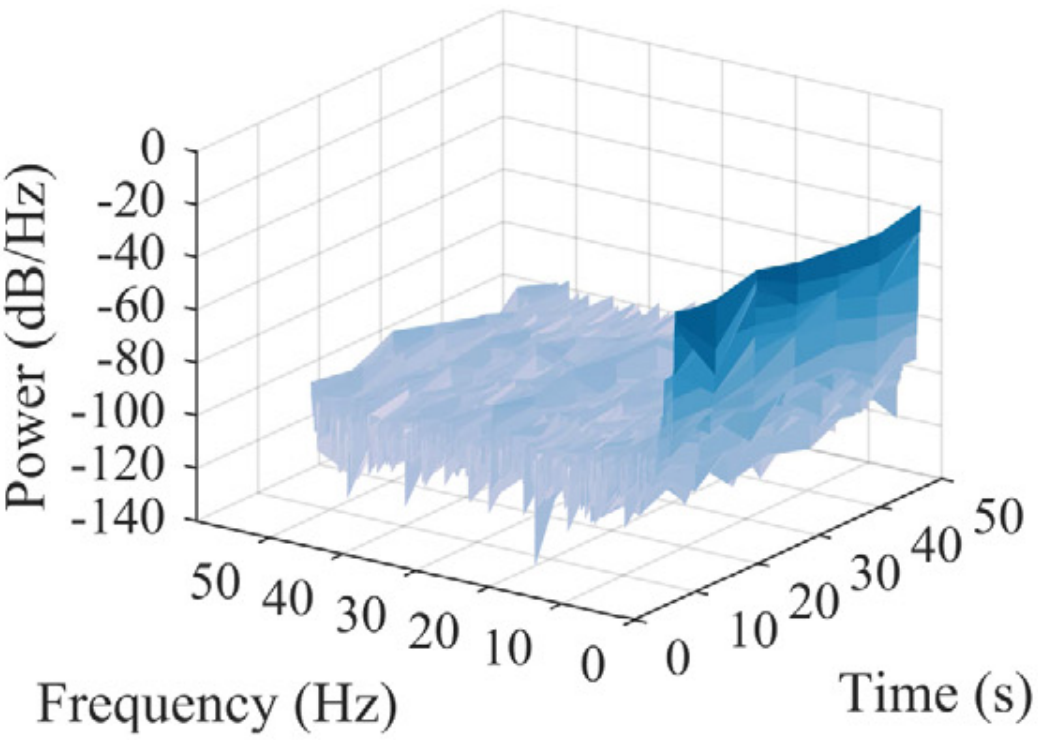
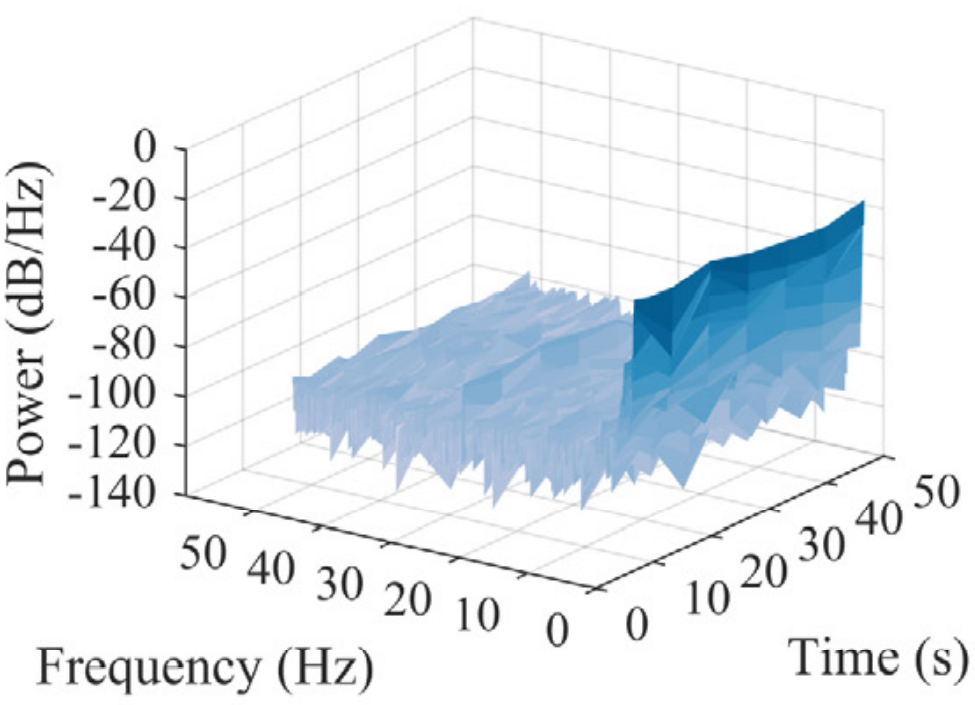
网络训练过程中位移重构情况如图8所示。右侧一列为位移响应在短时傅里叶变换后的时频分布。低频成分的重构迅速被网络学习掌握。之后,随着训练进行,高频成分的重构逐渐被学习。
| 
|
(a) 有限元模型计算值 |
| 
| 
| 
|
| 
| 
| 
|
(b) Epoch=1 | (c) Epoch=10 | (d) Epoch=100 | (e) Epoch=150 |
图8 不同训练阶段网络重构位移时域和频域分布
3.2 三跨连续梁
3.2.1 网络训练与重构
在简支梁的基础上,本文再应用一个三跨连续梁模型进一步讨论方法性能。模型和传感器布置如图9所示,连续梁跨径分布为:6+12+6=22m。有限元模型划分为44个单元,总共130个自由度。以前述类似方式施加交通荷载并生成训练用数据集。

图9 桥梁模型和传感器布置
桥梁中跨跨中和左边跨跨中位移重构结构如图10。
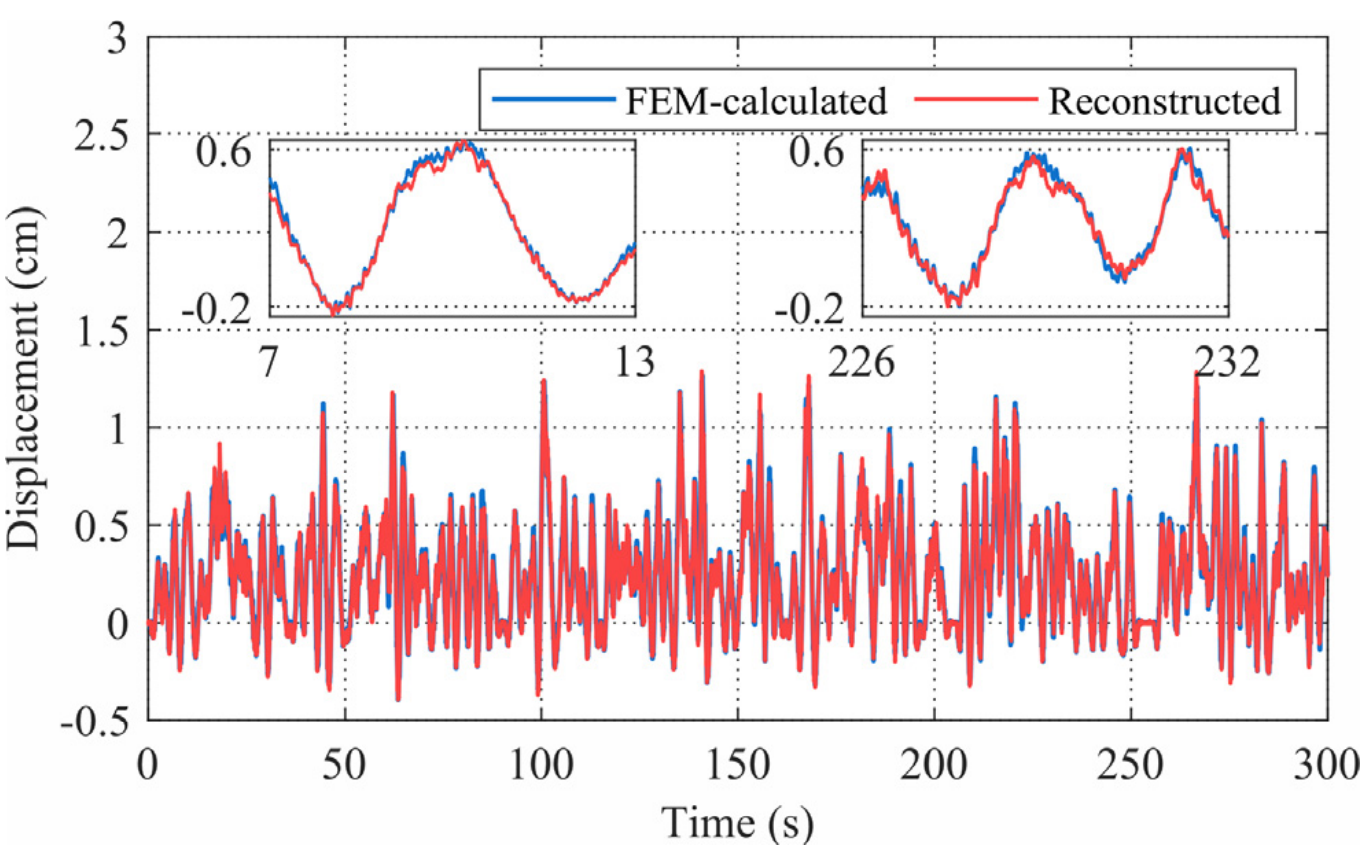
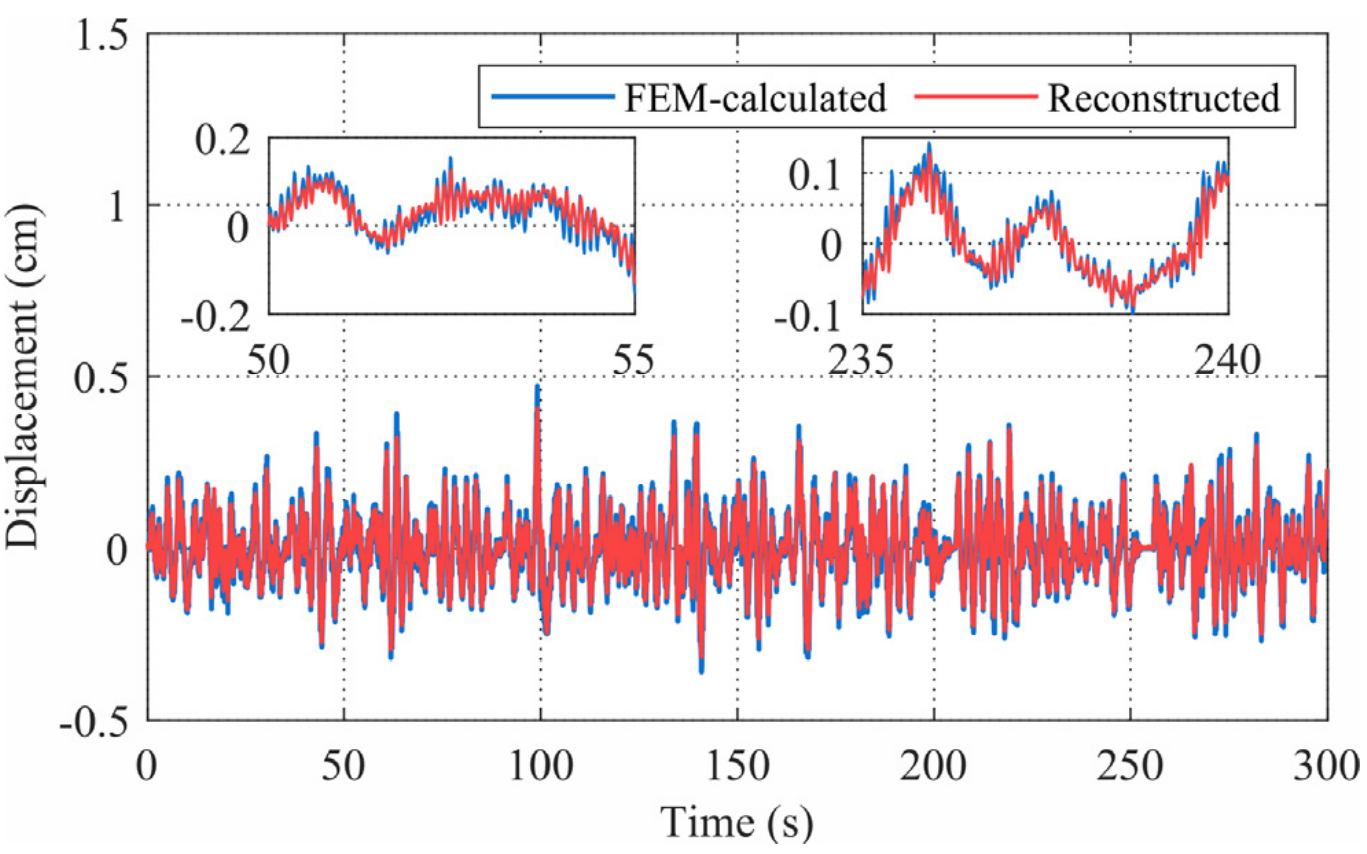
(a) 22号节点(跨中)位移重构 (b)6号节点(左边跨跨中)位移重构
图10 位移重构结果
3.2.2 噪声影响和物理损失项权重
对应变和位移数据分别加入10%的高斯噪声,并依次设置β参数为0,2×10-8,5×10-8和5×10-7,以此观察测试方法的鲁棒性和物理损失项的作用。结果显示,随着β参数依次改变,重构结构平均相对误差依次为3.29%,2.75%,2.47%,和3.35%。这说明当权重设置合理时,物理损失项可以帮助提高网络性能和鲁棒性,但是过大的权重反而会产生负面影响。不同权重参数β下模型重构的动态位移成分误差如图11所示,同样体现了物理导引损失项的作用。
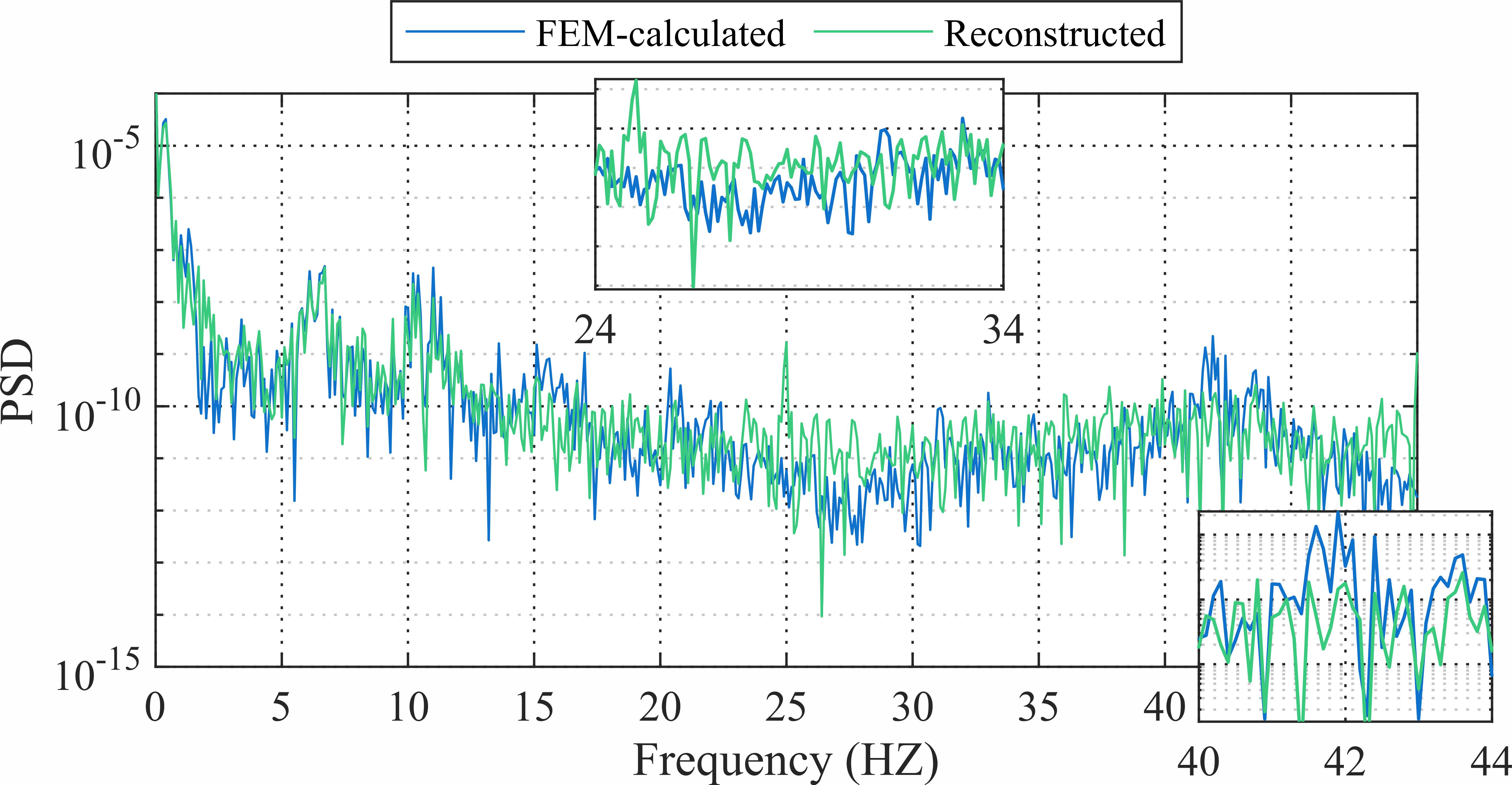
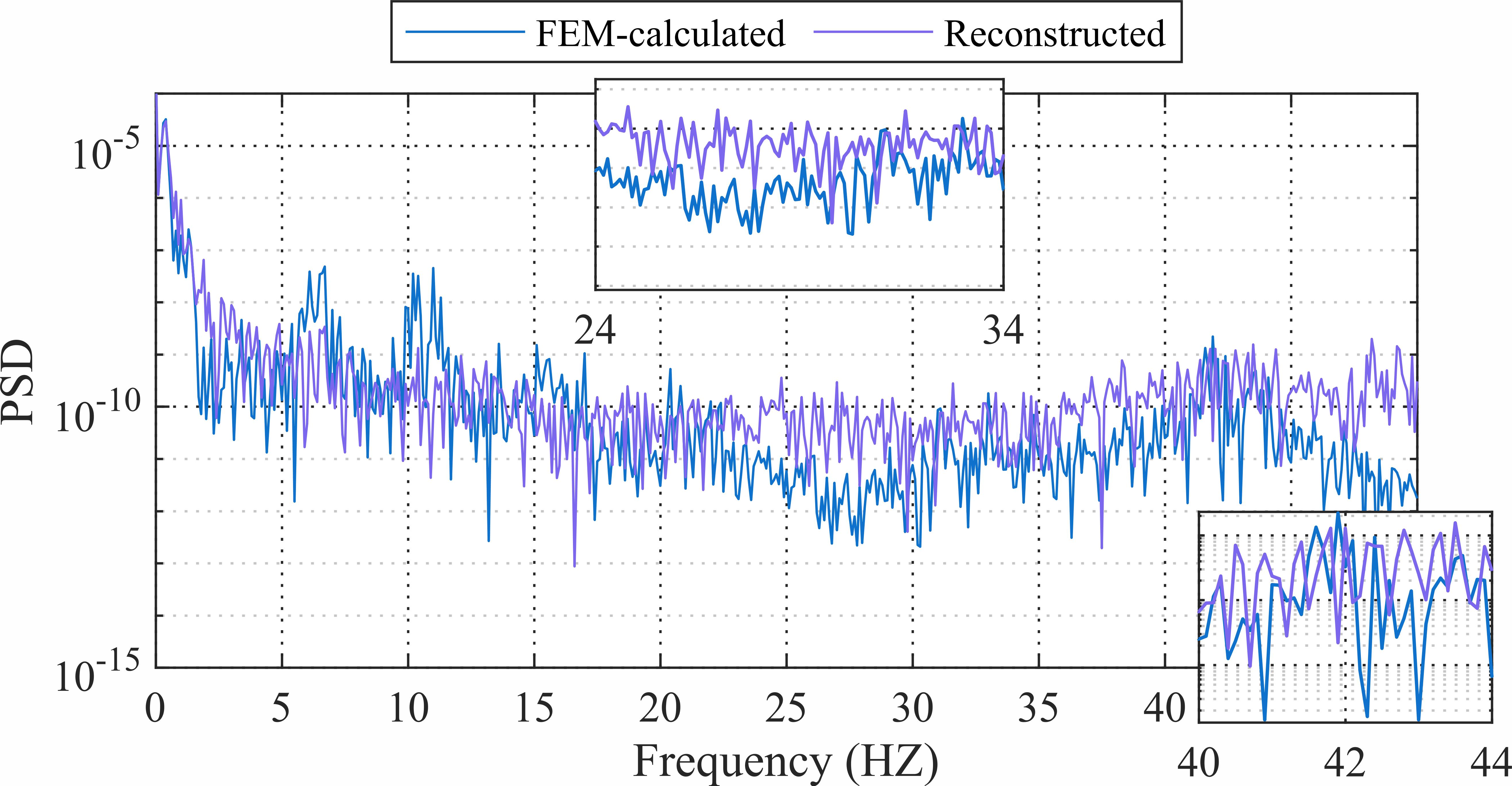
不同的β取值下重构位移和真实值频谱如图12所示。在β取值合理情况下,引入物理损失项可以使重构位移的频谱整体上更加精确,尤其在27Hz和42Hz附近。但当β取值过大,也反而会带来负面效果。
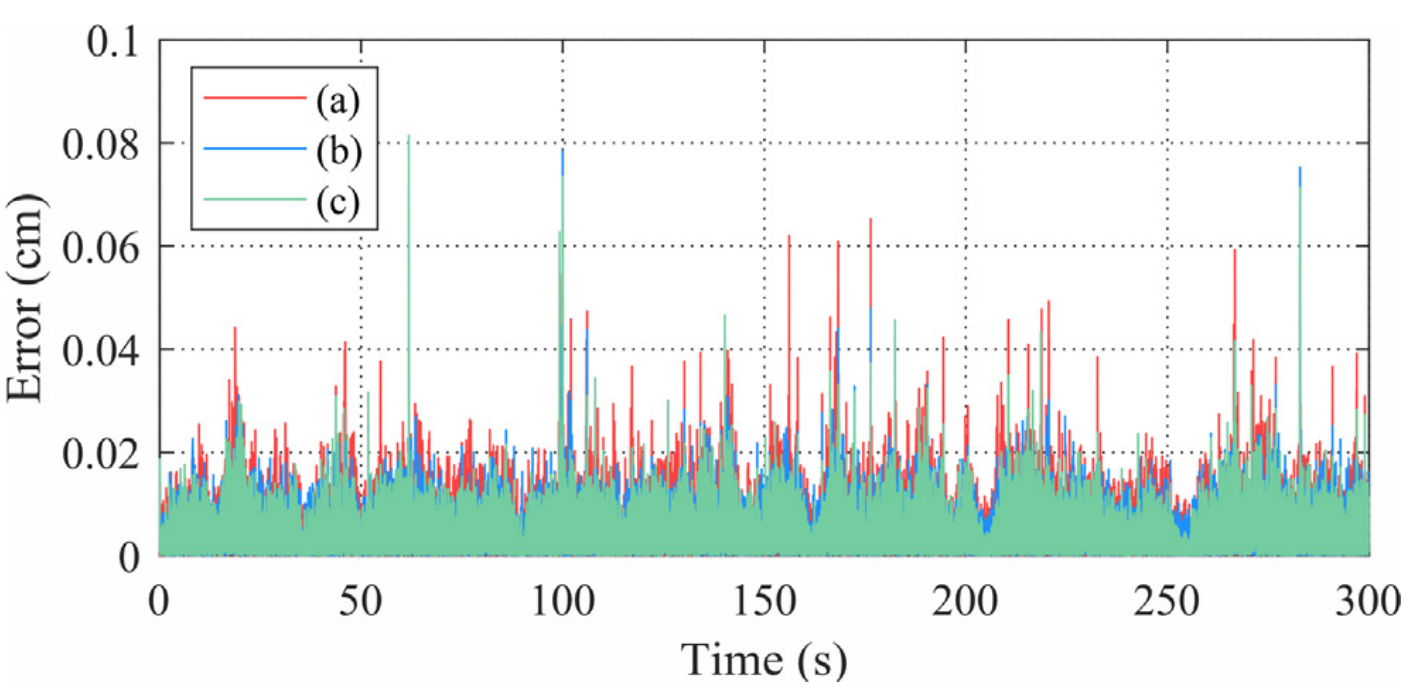
图11 不同模型重构动态位移的绝对误差:
(a) 无物理损失项,(b) β=2×10-8,(c)β=5×10-8
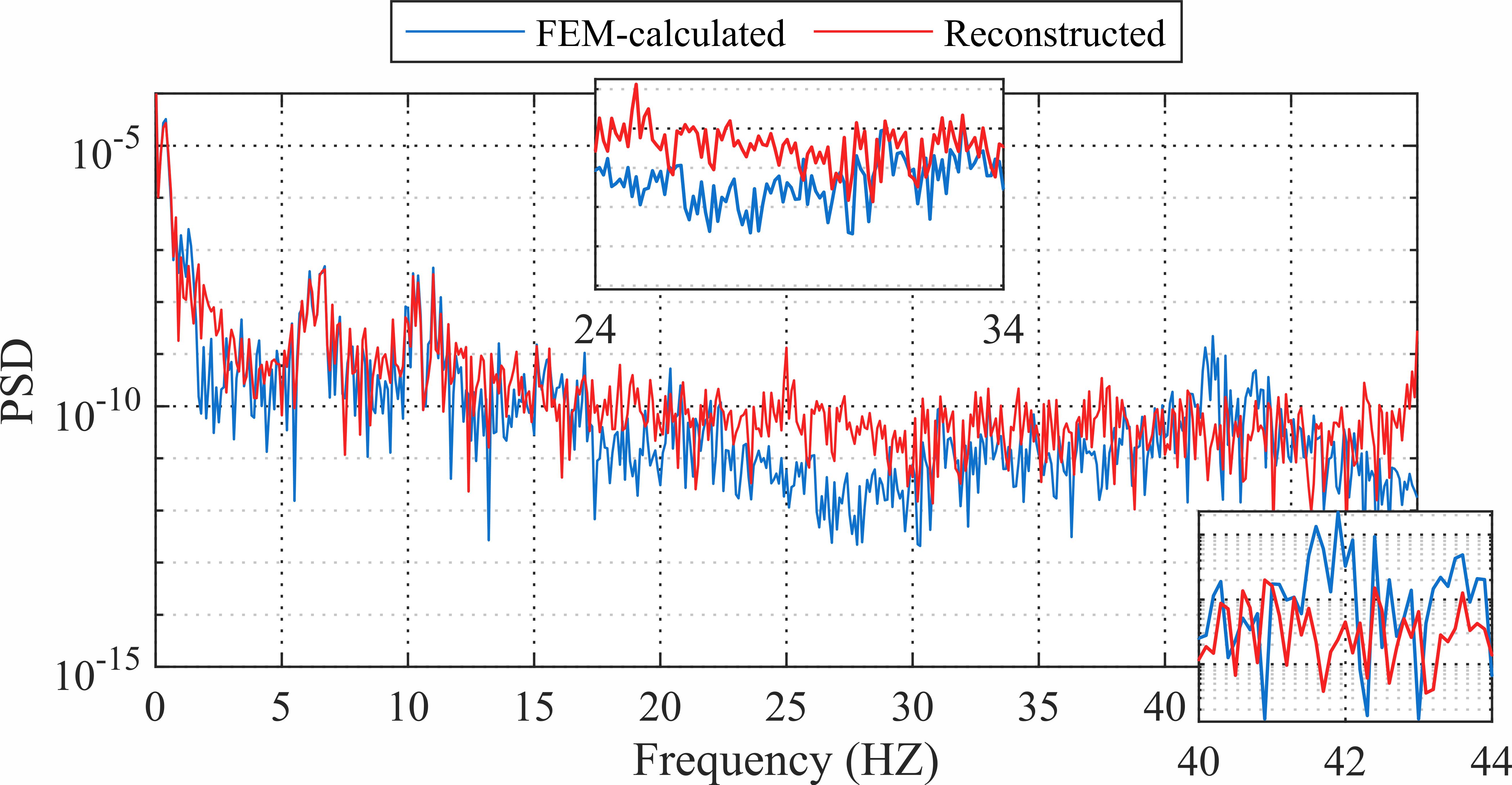
| 
|
(a) 无物理损失项(β=0) | (b) β=2×10-8 |
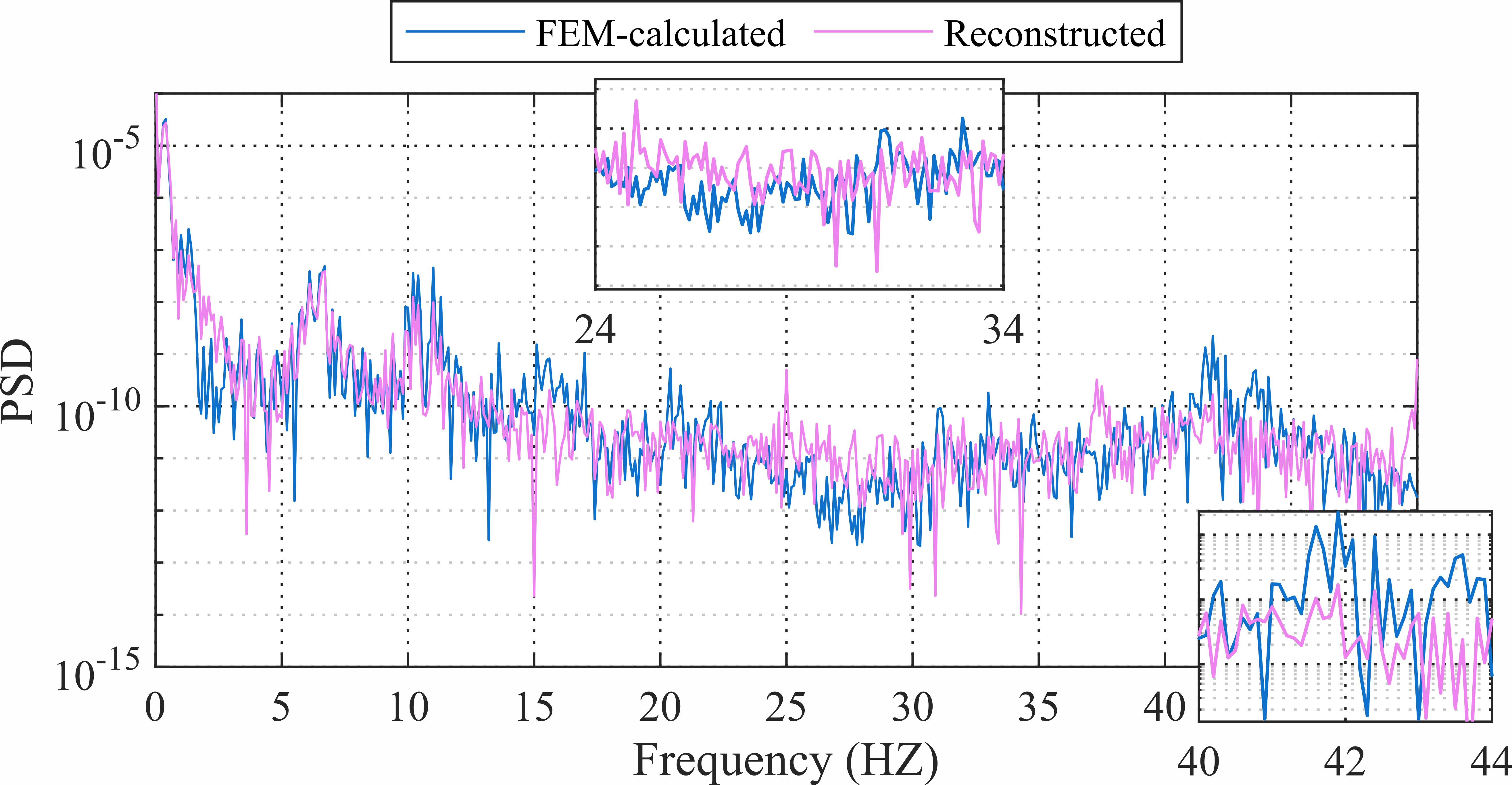
| 
|
(c) β=5×10-8 | (d) β=5×10-7 |
图12 不同β重构位移PSD
3.2.3 输入响应种类
除了将应变和加速度作为网络输入外,网络的输入响应组合可以有其他的选择。比如应变响应和速度响应组合,或转角响应和加速度响应组合。此处,转角和加速度响应作为输入,转角计安装在左侧第二个支座处。重构结果如图13所示,应用此种输入组合重构的结果同样具有较好的精度。同时,对比图13(a)和图13(b), 其误差分布不同。进一步地,可将应变、转角响应融合,伴随加速度响应一起输入到网络,可以得到更精确的重构结果,如图13(c)所示。
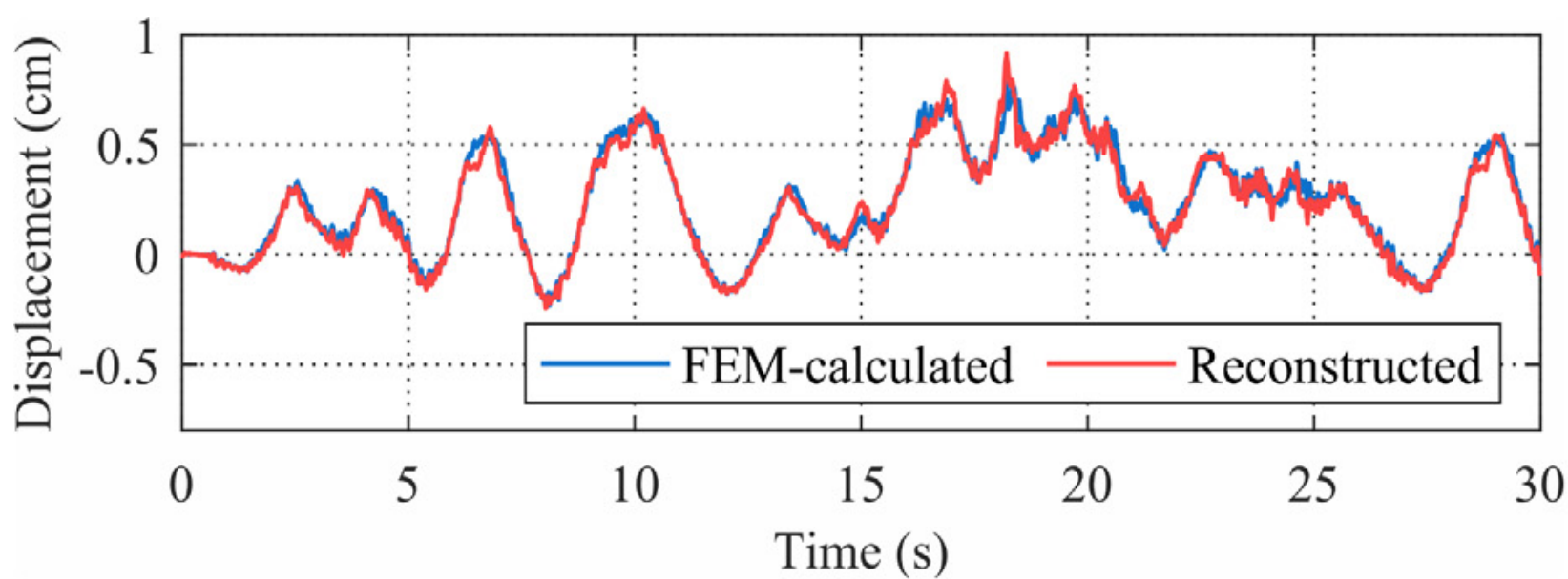
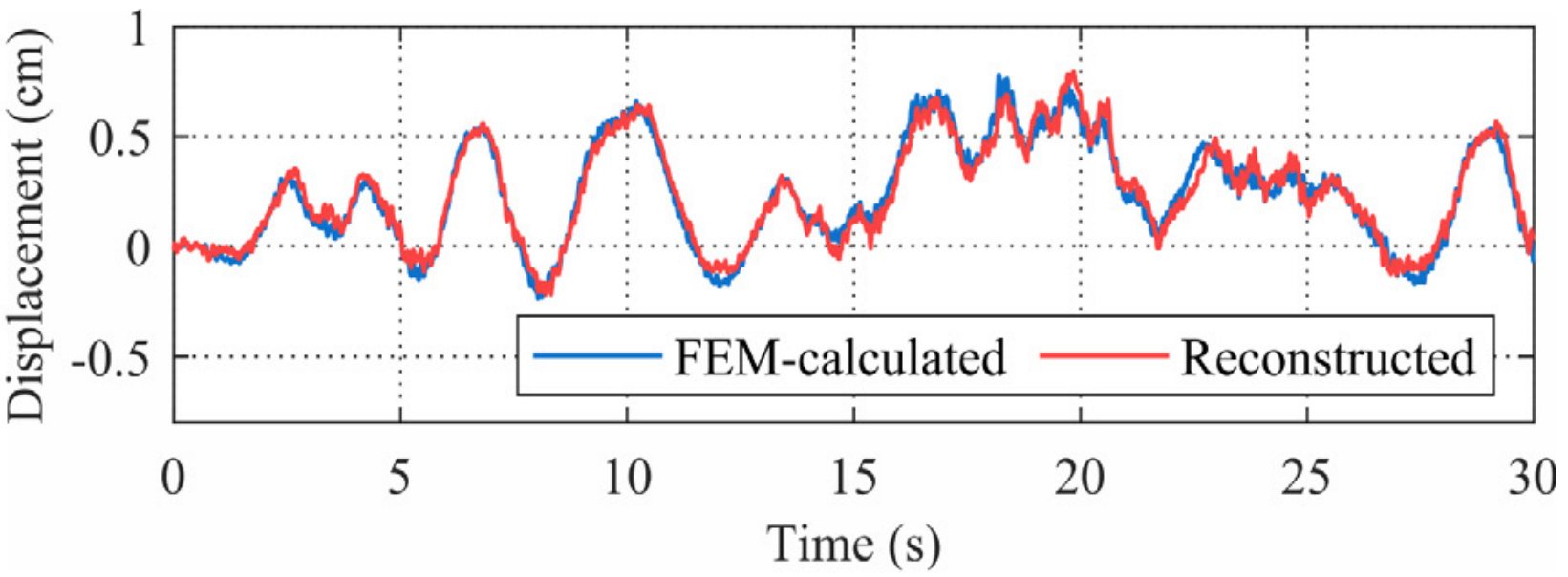
(a) 加速度和应变输入 (b) 加速度和转角输入
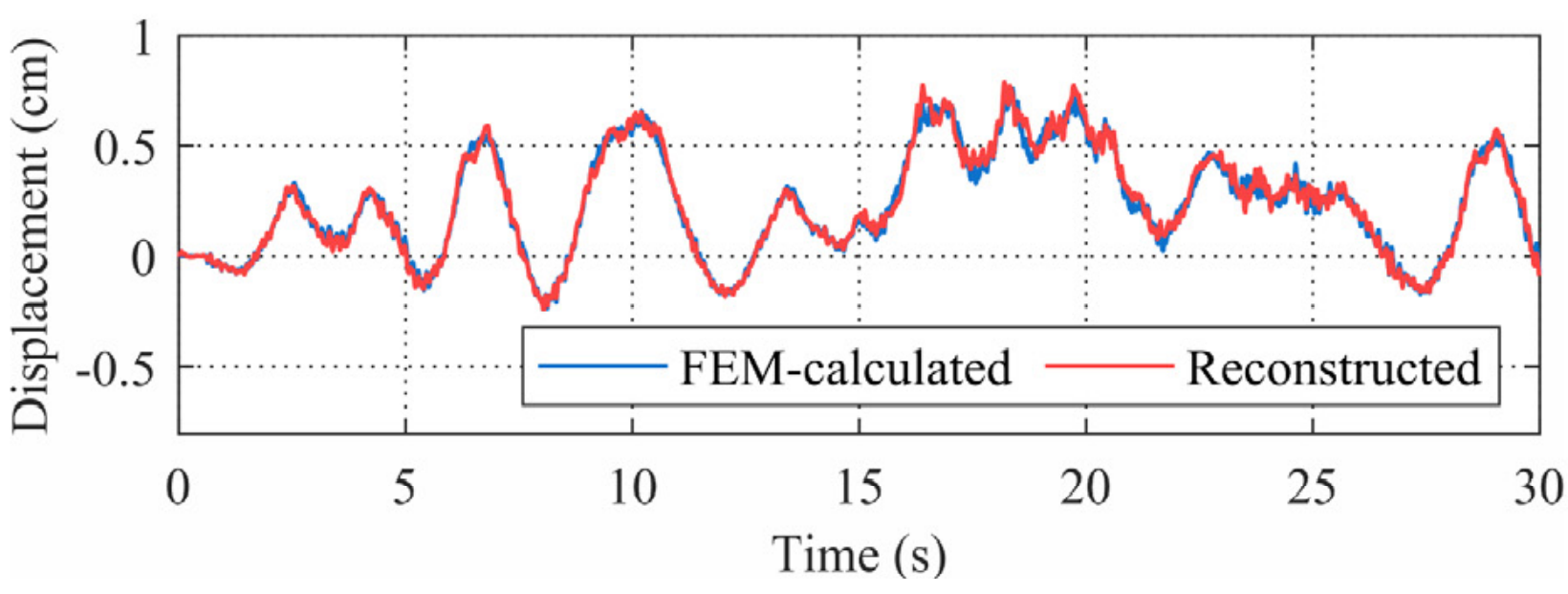
(c) 加速度、应变和转角输入
图13 不同输入响应组合下位移重构结果对比
4. 试验验证
本文进一步通过实验室缩尺模型验证方法。模型为一三跨连续梁,跨径分布为3×1m。梁跨中安装了加速度计、应变计和激光位移计,采样频率为200HZ。 荷载施加方式为:模型车装载随机重量的负重片,以随机匀速通过桥梁,同时使用锤子在模型车附近随机敲击。试验布置如图14所示:

图14 试验布置
应用所提出的方法重构跨中位移,位移重构结果如图15所示。重构的位移与测量值符合较好,平均相对误差为1.95%,图16展示了在频域上重构的效果。可以看出,在频域上位移的主频成分也能够较好地重构,尤其是接近0HZ的准静态成分和接近一阶自振频率(41Hz)位置处。
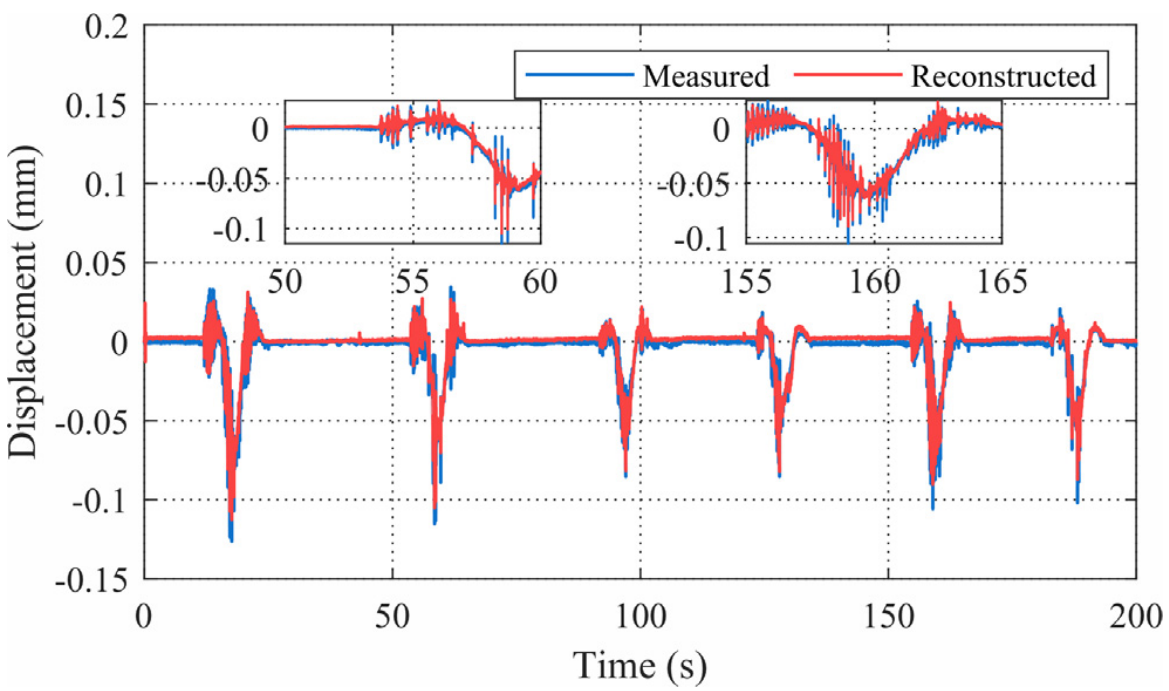
图15 桥梁跨中位移重构结果
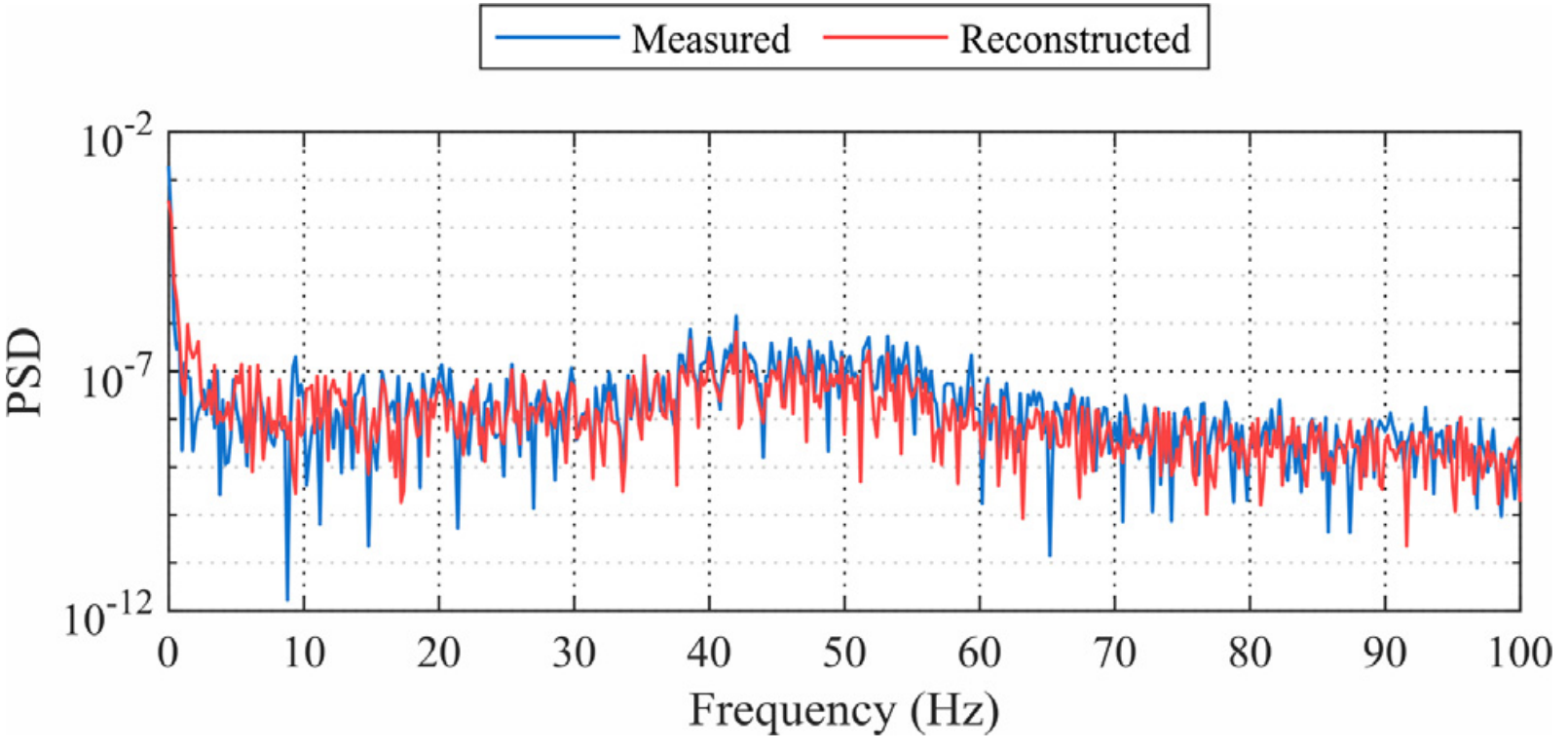
图16 测量位移和重构位移频谱对比
由于荷载不易控制,且测量数据包含噪声,试验情况比数值模拟更加复杂,即便如此,本试验依旧可以体现所提出的方法框架在真实结构上的可行性。
5. 结论
本研究提出了一种基于物理导引的深度学习方法重构桥梁车致位移响应。通过物理导引下设计的网络结构和损失函数,准静态和动态位移成分都可以被较好地重构。除此之外,网络输入响应类型可灵活选择变动。通过数值模拟案例和实验室模型验证了方法的性能和应用在真实桥梁结构的潜力。
6. 参考文献
[1] Thong YK, Woolfson MS, Crowe JA, Hayes-Gill BR, Jones DA. Numerical double integration of acceleration measurements in noise. Measurement 2004;36:73–92.
[2] Stiros SC. Errors in velocities and displacements deduced from accelerographs: An approach based on the theory of error propagation. Soil Dyn Earthquake Eng 2008;28:415–20.
[3] Park JW, Sim SH, Jung HJ. Displacement Estimation Using Multimetric Data Fusion. Ieee-Asme Trans Mech 2013;18:1675–82.
(更多详细内容可参考实际文章)