由于建模、参数和信号传输的误差，初始有限元模型在静、动力特性方面与实际结构存在差异。有限元模型修正（FEMU）旨在通过调整模型参数来减少FE模型与现有结构之间的差异。不断发展的结构健康监测（SHM）技术大大促进了FEMU的数据获取。

联合测量的静态和动态数据可以扩大FEMU的目标信息，是提高FEMU精度的有效手段。Xiao、Wang等[1,2]将静力测量数据（如影响线、静力位移、应力）融入修正目标，修正后桥梁在静、动力特性上都取得较好的表现。虽然SHM技术可以为FEMU提供足够的数据，但静态数据仍然必须通过现场静力试验获得，这一过程需要中断交通和提前筹备跑车试验，为模型修正带来了不便。为简化静态数据的获取，我们提出另外一种静力数据的获取思路：将设计试验中的车辆荷载转化为确定运营阶段下的车辆荷载，如此便避免了实桥试验，降低了获得准确静态数据的难度。

最近的车辆载荷识别方法为上述思路提供了充分的技术支持。Jian、Ge等人[3,4]分别提出了基于计算机视觉的运营阶段桥面荷载识别技术，包括加载位置、轴重、速度和车辆类型等信息都可以通过该方法得到准确识别。

本文的主要贡献在于以下几个方面：1）提出了一种基于监测和计算机视觉技术的联合静动力FEMU方法。实测静态数据通过回归方法从监测数据中提取，理论静态数据通过车辆载荷识别和FE仿真模拟获取。提出的方法避免了传统的FEMU方法在获取静力数据上的不便。2）提出了一种考虑到静力响应的整体形状和极值差异的误差指标的计算方法。3）采用并行粒子群优化算法（PSO）寻找修正参数的全局最优解。在一个带有健康监测平台的三跨连续箱梁桥上开展了模型试验研究，利用四个试验场景的数据验证了所提出的FEMU方法的有效性。

2.研究方法

2.1 提出的有限元模型修正方法

图1展示了提出FEMU方法的流程，该流程包括监测数据预处理、理论响应计算、目标函数建立和目标函数优化这四部分。在数据预处理中，通过模态识别方法（随机子空间识别），从试验加速数据中识别出结构测量模态，使用局部加权回归和平滑散点图（LOWESS）方法从监测数据中提取测量的静力响应。在目标函数优化部分，建立了并行PSO算法，极大地提升了优化速率。在本节后文的内容中，将对理论静力响应计算和目标函数建立进行详细介绍。

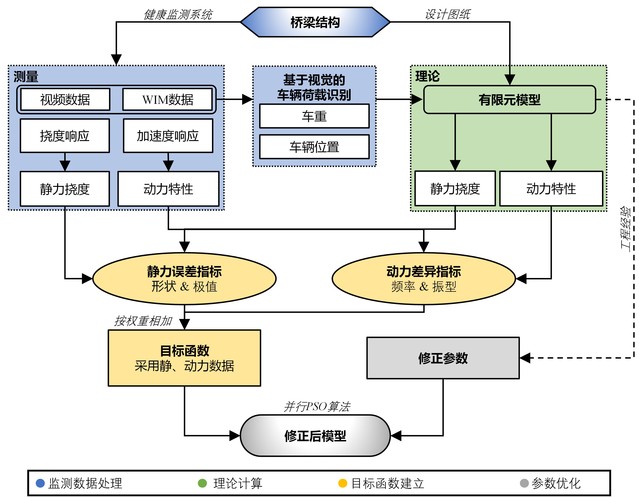
图1 提出的有限元模型修正方法的流程

2.2 车致静力响应模拟

本文基于计算机视觉（CV）、动态称重（WIM）的车辆荷载技术和FE仿真实现了车致静力响应计算，相应流程如2所示。车辆荷载识别技术为有限元模型加载提供了荷载输入信息（包括荷载位置和荷载值），随后在有限元模型中准确模拟结构静力响应。

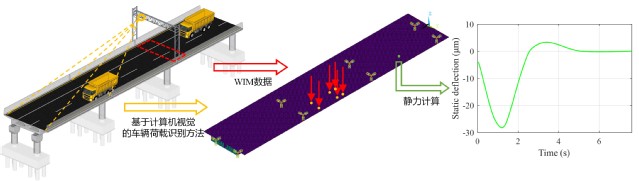
图2 车致静力响应模拟流程

2.3 修正目标函数

修正目标函数F(θ)由静力差异指标（SEI）和动力差异指标（DEI）两部分组成，如公式1所示。式中，θ为修正参数向量，n为静力加载次数，k为考虑的总模态阶次。α₁和α₂分别代表两类指标的权重，可根据实测数据的准确程度进行调整。

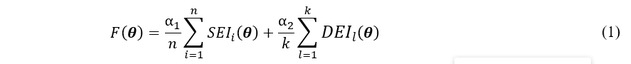
其中，静力差异指标（SEI）由静力响应形状差异（DDS）和静力响应极值差异（DED）组成，如公式（2）-（4）所示。β₁和β₂分别指两类指标的权重，m代表响应中的极值点个数，Y指静力响应，下标M和T分别指实测、理论数据。

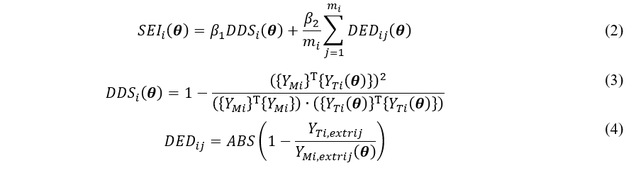
图3对比了四个具有不同静态误差指标的模拟静态响应与测量静态响应（β₁=β₂=0.5）。结果表明，当SEI值小于0.2时，静态响应与测量的相对匹配，因此可用0.2的阈值来判断理论上的静态响应是否满意。

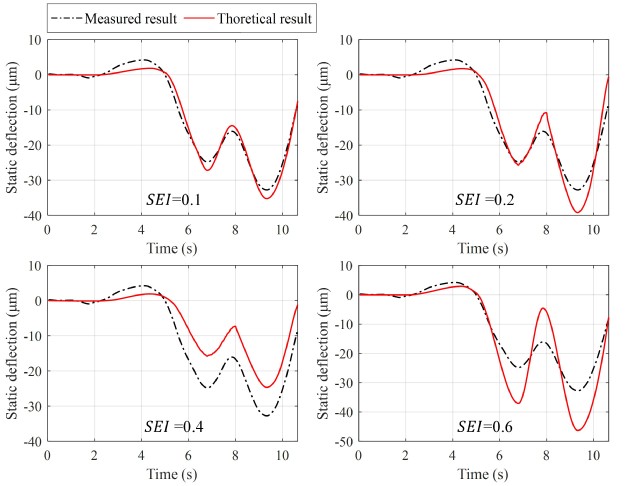
图3 不同静力差异指标下的静力响应对比

动力差异指标（DEI）由频率差异（DF）和振型差异（DMS）组成，如公式（5）-（7）所示。式中，f代表频率，Φ代表振型。

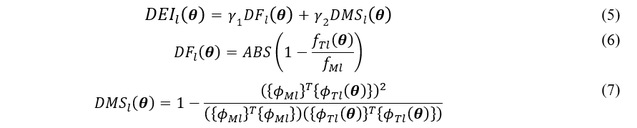
3.试验验证

3.1 试验设计

为了验证和评估所提出的FEMU方法的有效性，在一个带有健康监测平台的三跨连续箱梁模型桥上进行了跑车试验。桥梁的跨径布置为1m×3=3m，在桥梁上安装了摄像头、加速度计和位移计等传感器。模型桥尺寸和荷载传感器布置如图4所示。

图4 传感器布置示意图

试验中采用两辆三轴遥控卡车作为车辆模型。卡车可以进行前进、后退和转向操作。我们在试验中模拟了单车直行（工况I）、单车变道（工况II）、双车直行（工况III）、双车变道（工况IV）四种车辆行驶工况，试验的现场设置及传感器信号如图5所示。

图5 试验现场布置及监测信号示意图

3.2 模型修正结果

本文选取了主梁的弹性模量、材料密度和支座抗弯刚度参数作为修正参数。采用工况I和工况IV的试验数据做模型修正，分别得到修正后的模型I和模型IV。在并行PSO算法中，种群大小设置为48，迭代次数为300次，优化迭代过程如图6所示。

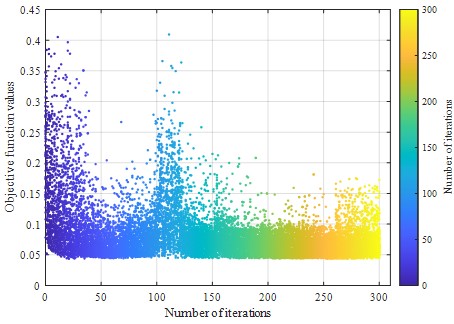
图6 修正算法迭代结果

表1和图6展示了修正后模型的第一阶模态数据，与最初的FE模型相比，更新后的模型在动态特性方面与实际结构更为接近。

表1 不同方法得到的结构动力特性

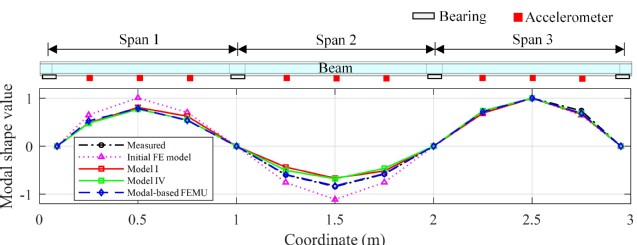
图7 各类方法的模态结果

图8展示了修正后模型在工况I下静力响应计算结果，可以看出修正后模型在响应形状、极值方面均与实测响应更为接近。

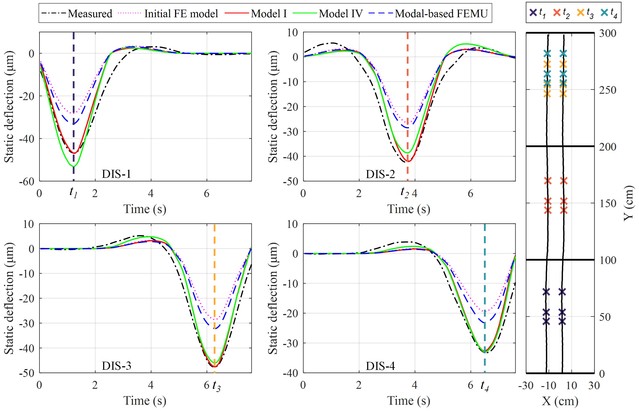
图8 各类模型在工况I中的静力计算结果

图9展示了各类模型在各工况下的静力差异指标，可看出模型I和模型IV的静态误差指标均小于阈值0.2，且小于初始模型的静态误差指标，这证明无论使用复杂还是简单驾驶场景的数据，所提出的方法都能在一定程度上改善模型的静态特性。值得一提的是，采用模型I计算其他工况下的静力响应数据，响应准确程度都得到了提高，证明修正后模型可应用于各类场景下的结构静力响应计算。

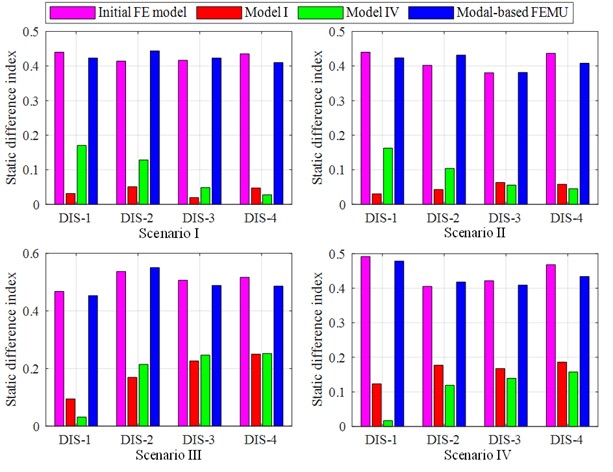
图9 各类模型的静力差异指标对比

4.结论

本文提出了一种使用交通视频数据和结构响应来丰富修正目标的模型修正方法。采用运营阶段交通荷载作用下的结构动力特征和静力响应来建立FEMU的目标函数。在一个带有健康监测系统的模型桥上开展了多个工况试验，验证了本文提出方法的适用性和准确性。本研究得出的结论总结如下：

 (1）所提出的FEMU方法基于计算机视觉的车辆荷载识别技术，直接利用运营阶段的海量、多源数据来修正有限元模型，避免了获取静态数据时中断交通造成的经济损失、人力损失和时间损失。大大提高了使用静态和动态数据的FEMU方法的适用性。

 (2）提出的静态误差指数能够描述静态响应的极值特性，考虑了静态响应的曲线形状差异和极值差异。

 (3）采用提出方法修正后的模型可以模拟修正过程中未使用测点的静力响应，理论结果与测量结果吻合良好。同时，验证工况表明，通过提出的方法更新的FE模型可以准确地模拟其他车辆行驶工况下的静力位移。因此，采用本方法修正后的FE模型可以准确地模拟整桥在各类车辆行驶工况下的静力响应。

5.参考文献

[1] Xiao X, Xu YL, Zhu Q. Multiscale Modeling and Model Updating of a Cable-Stayed Bridge. II: Model Updating Using Modal Frequencies and Influence Lines. J Bridge Eng. Oct 2015;20(10)doi:Artn 0401411310.1061/(Asce)Be.1943-5592.0000723.

[2] Wang Y, Li Z, Wang C, Wang H. Concurrent multi-scale modelling and updating of long-span bridges using a multi-objective optimisation technique. Struct Infrastruct E. 2013/12/01 2013;9(12):1251-1266. doi:10.1080/15732479.2012.683198.

Jian XD, Xia Y, Lozano-Galant JA, Sun LM. Traffic Sensing Methodology Combining Influence Line Theory and Computer Vision Techniques for Girder Bridges. J Sensors. 2019;doi:Artn 340952510.1155/2019/3409525.

[3] Ge LF, Dan DH, Li H. An accurate and robust monitoring method of full-bridge traffic load distribution based on YOLO-v3 machine vision. Struct Control Hlth. Dec 2020;27(12)doi:ARTN e263610.1002/stc.2636.

（更多详细内容可参考实际文章）