1. 研究背景

拉索是索承重桥梁的核心构件之一，索力反映了拉索自身乃至整个桥梁的受力状态。因此，在桥梁运营过程中，索力检测至关重要。

振动法是索力检测中使用最广泛的方法。该方法首先测量拉索振动的加速度或位移时程，再从中提取出各阶模态频率，最后选取合适的拉索动力学模型来计算拉索张力。对于大型斜拉桥的长索而言，其垂度和刚度可以忽略，因此可以由张紧弦理论得到索力与特征频率之间的显式关系。

传统的振动法通过加速度计或位移计来测量拉索的振动，然而安装这些仪器非常费时费力。因此，一些学者尝试用新型非接触式传感器来代替传统仪器。微波雷达就是其中的代表，该设备可以同时测量多条拉索的位移时程，且安装方便、精度较高。

然而微波雷达的引入也为拉索的大批量快速索力识别提出了新的课题。一方面，尽管前人的许多研究已经证明了用微波雷达进行索力识别的可行性，但并未提出一种自动化处理算法，为了计算索力，通常需要人工干预来选出各阶模态频率和对应的模态阶次。另一方面，由于微波雷达可以同时测量多条拉索的位移时程，因此即使是单次测量后也会有大量数据需要处理，人工干预将非常费时费力。

本文的主要贡献便是设计了一套索力识别方法，实现了大批量拉索振动数据的自动化处理，从而可以更好地发挥微波雷达在索力识别中的强大性能。本文的具体内容又可分为以下几个方面：1）提出了快速筛峰算法FSM用于自动提取拉索位移频谱的各阶模态频率。2）提出了加权哈希投票算法WHV用于自动判定各阶模态频率对应的模态阶次。3）将FSM和WHV等算法加以整合，提出了一套完整的通过位移时程计算拉索索力的方法，并通过实桥测试证明了该方法的可行性与高效性。

2. 自动化算法

基于微波雷达的索力计算主要分为以下步骤（图1）：1）用微波雷达测得拉索振动的位移时程。2）通过快速傅里叶变换得到频谱。3）利用高通滤波器过滤低频噪声。4）利用快速筛峰算法FSM识别各阶特征频率。5）利用加权哈希投票算法WHV判定各阶模态频率的阶次。6）由张紧弦公式算得拉索索力。

图1 基于微波雷达的拉索索力检测流程图

2.1 快速筛峰算法FSM

快速筛峰算法FSM用于识别频谱中的各阶峰值（图2）。该方法基于滑动窗口，通过比较窗口内所有数据的大小来筛选极大值。

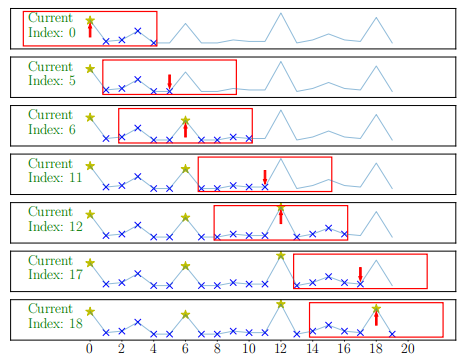
图2 FSM识别各阶特征频率

此外，用滑动窗口遍历整个频谱序列比较费时，为了降低时间复杂度，FSM引入了记事本数组以记录两两比较的结果。通过查看记事本数组先前的记录，可以跳过滑动窗口在遍历过程中的绝大部分位置（图2）。优化后的算法为线性时间复杂度，具体伪代码如图3所示。

 图3 FSM的伪代码

2.2 加权哈希投票算法WHV

在识别了各阶模态频率后（图2），还需求出其对应的模态阶次。加权哈希投票算法WHV首先计算拉索的名义基频（图4），并在此基础上计算各模态频率的阶次（图5）。

注意到长索的模态频率为等距分布，且相邻两阶特征频率之差即为基频。因此，WHV首先计算了特征频率的一阶差分序列。然后，对各个差分进行哈希映射并投票。最后找出得票最多的哈希值并加以解码，就得到了名义基频，具体流程如图4所示。

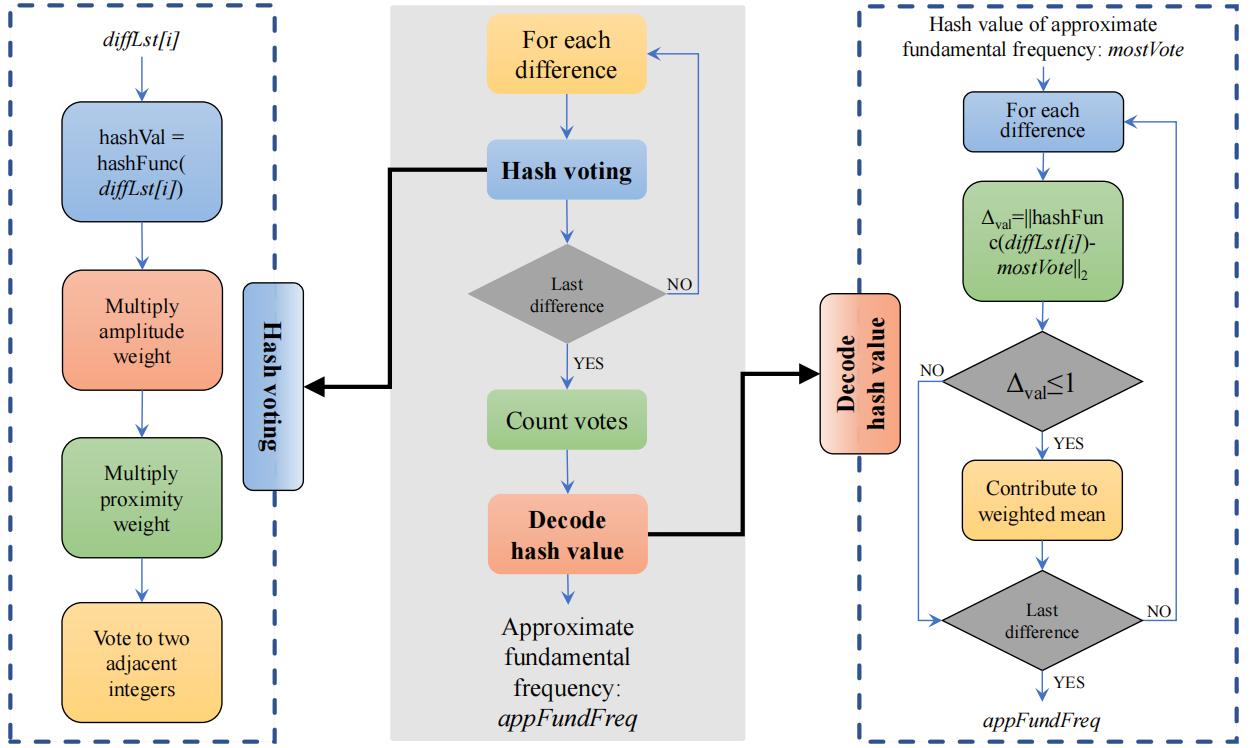
 图4 哈希投票求出名义基频的流程图

在求出名义基频后，可以据此来推算各阶特征频率的模态阶次：特征频率除以名义基频即为模态阶次。此外，WHV采用频率差分序列代替频率序列，避免了误差的累积（图5）。

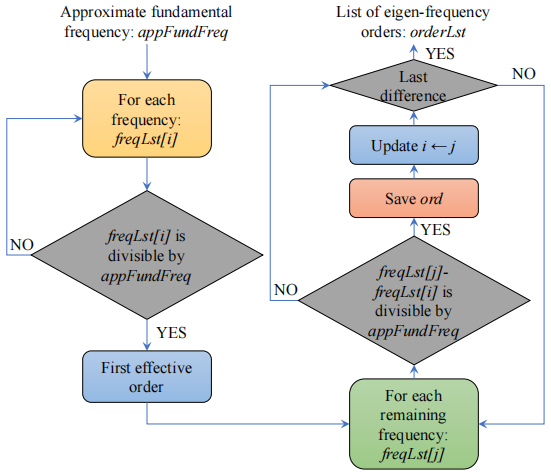
 图 5通过名义基频求出模态阶次的流程图

2.3 由模态频率求得基频

由于长拉索的垂度和刚度可以忽略不急，故可用张紧弦公式来计算索力。

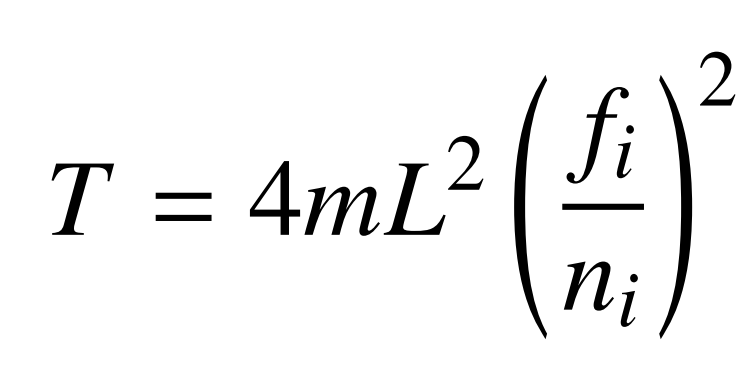
此外，由于基频易受环境噪声干扰，因此可用“频率-模态直线”的斜率来代替基频。该斜率可通过“频率-模态平面”上特征点的线性拟合得到。

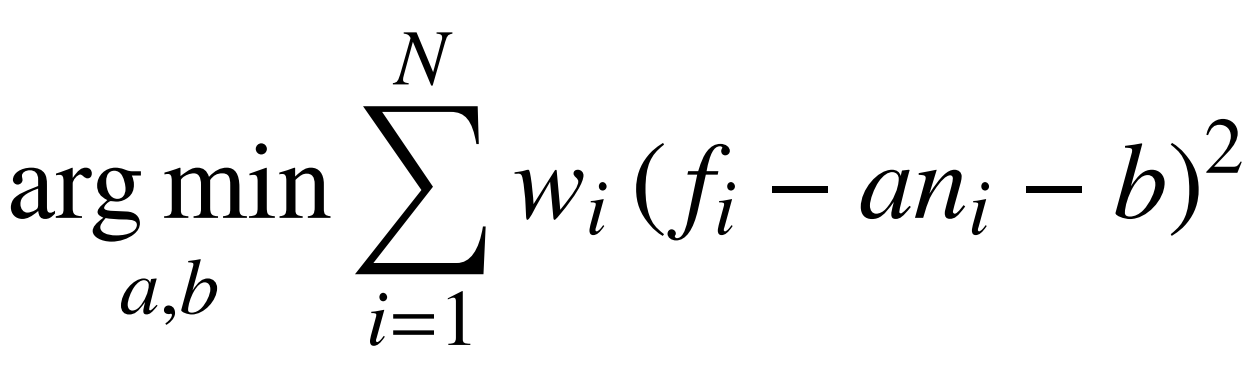
3. 试验验证

为了验证采用微波雷达进行索力识别的高效性与所提出算法的准确性，本研究在连接江西九江市与湖北黄梅县的鳊鱼州长江大桥上开展了实桥试验（图 6）。试验针对37个加载工况下的NM28-NM37索共10根斜拉索进行了索力测试。为了方便数据呈现，下面以第一个工况的数据处理为例进行介绍。

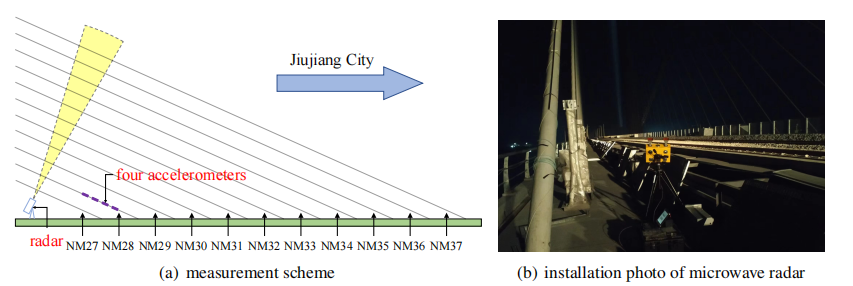
 图 6 微波雷达架设图

3.1 原始位移时程与频谱

由微波雷达测得的原始位移时程如图7所示。

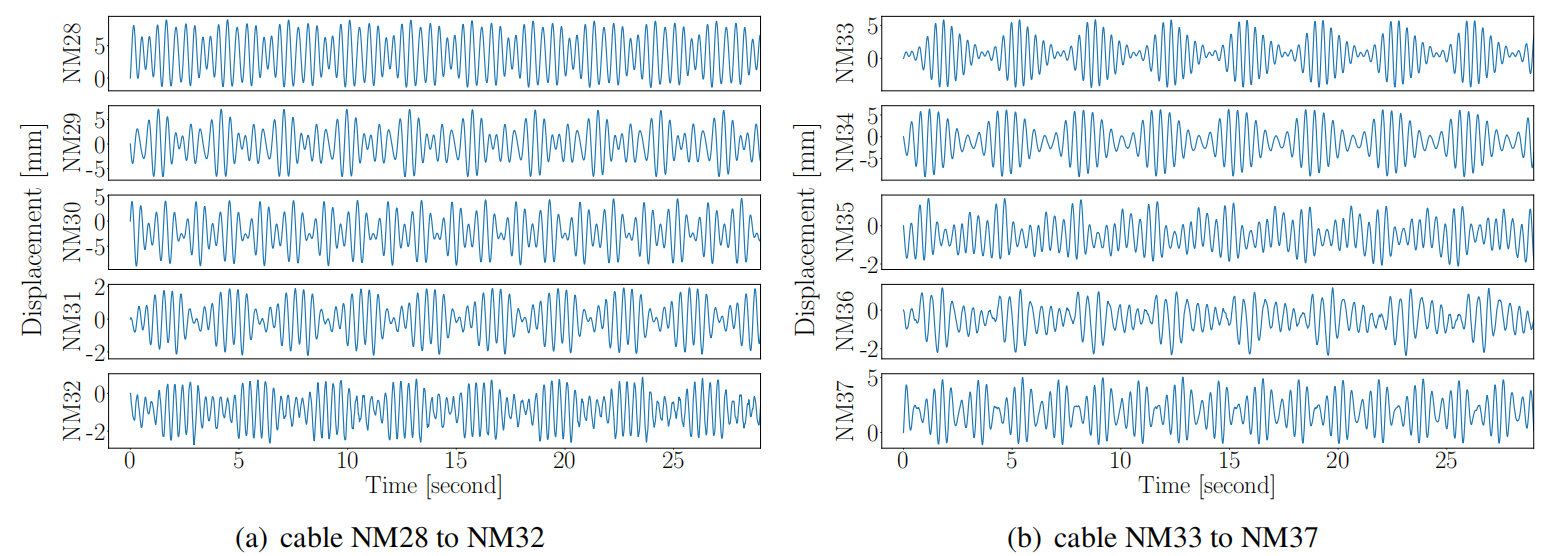
 图7 NM28-NM37索的原始位移时程

进行快速傅里叶变换并滤去低频噪声，得到频谱如图8所示。

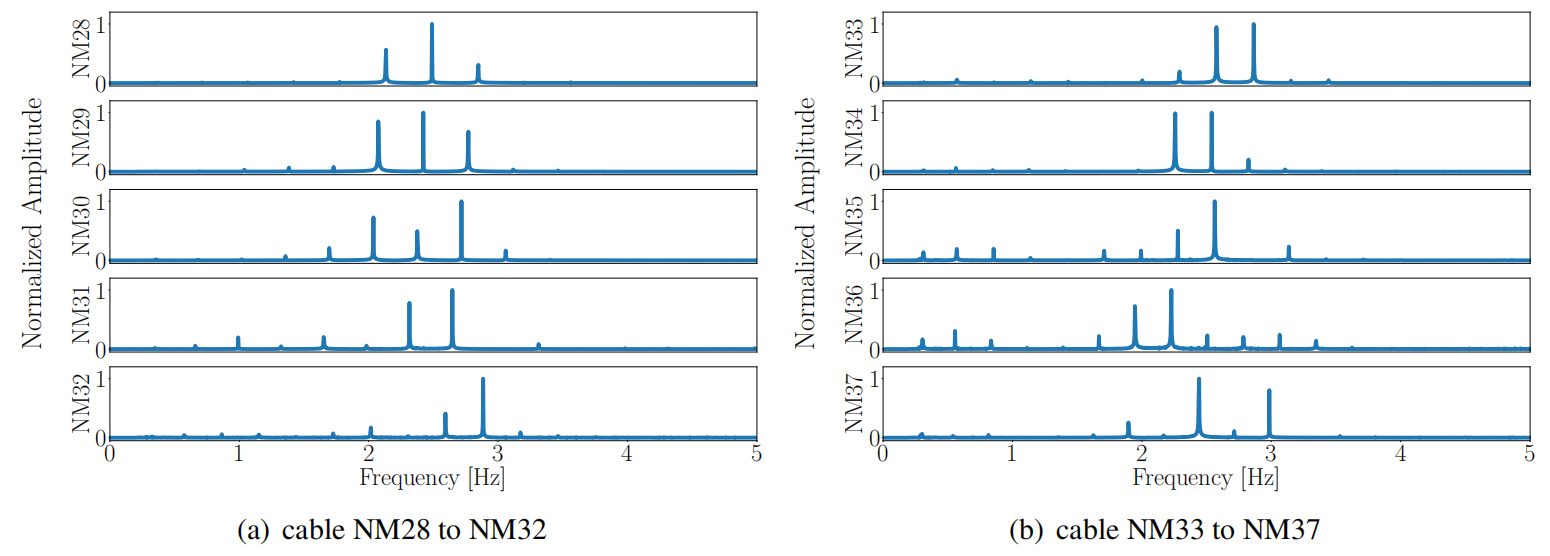
 图8 NM28-NM37索的频谱

3.2 模态频率提取与模态阶次判定

用FSM识别拉索的所有特征频率，图9展示了NM28索和NM37索的特征频率提取结果。

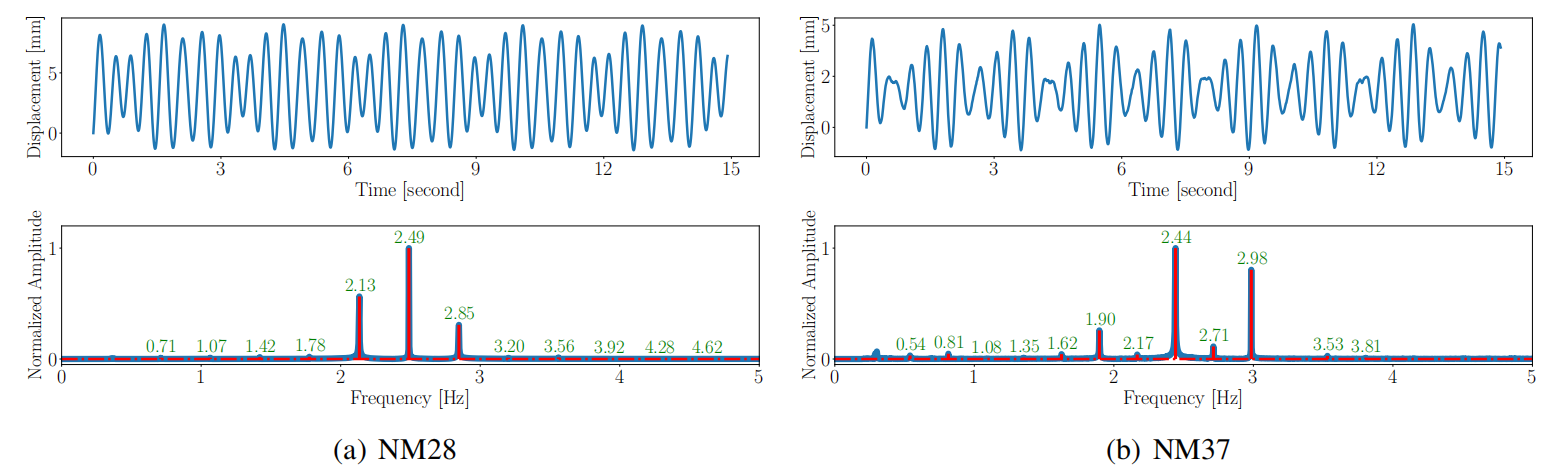
 图9 NM28索和NM37索的特征频率提取

用WHV判定识别所得的所有特征频率的阶次。并将所有特征频率及其对应的模态阶次标注于“频率-模态平面”之上（图10）。

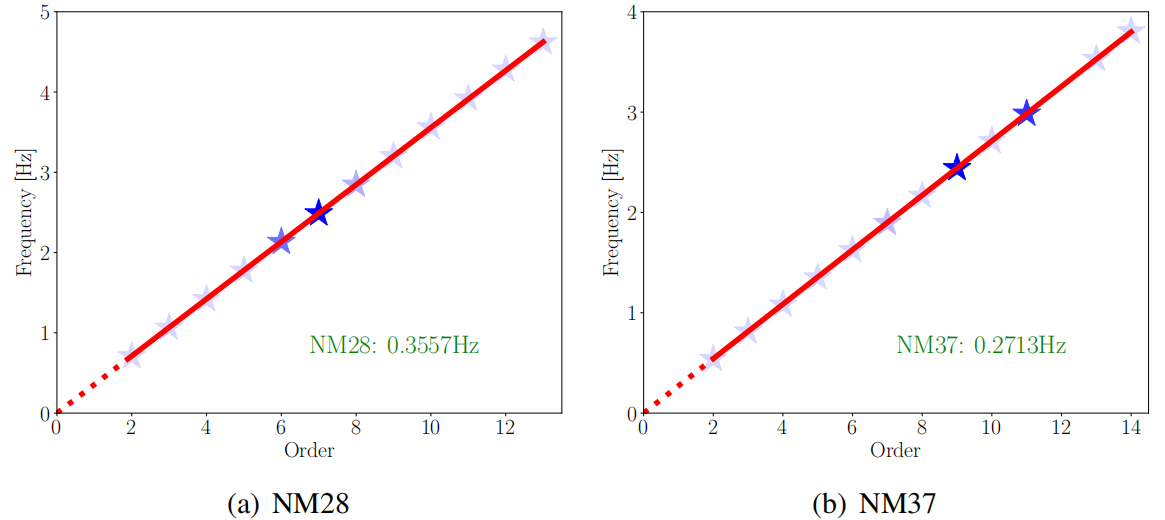
 图10 NM28索和NM37索的名义基频拟合

3.3 计算索力

对“频率-模态平面”上的所有特征点进行线性拟合，得到拉索的名义基频（图10）。最后，利用张紧弦理论计算索力。第一个工况下，NM28-NM37索的索力如图11所示。

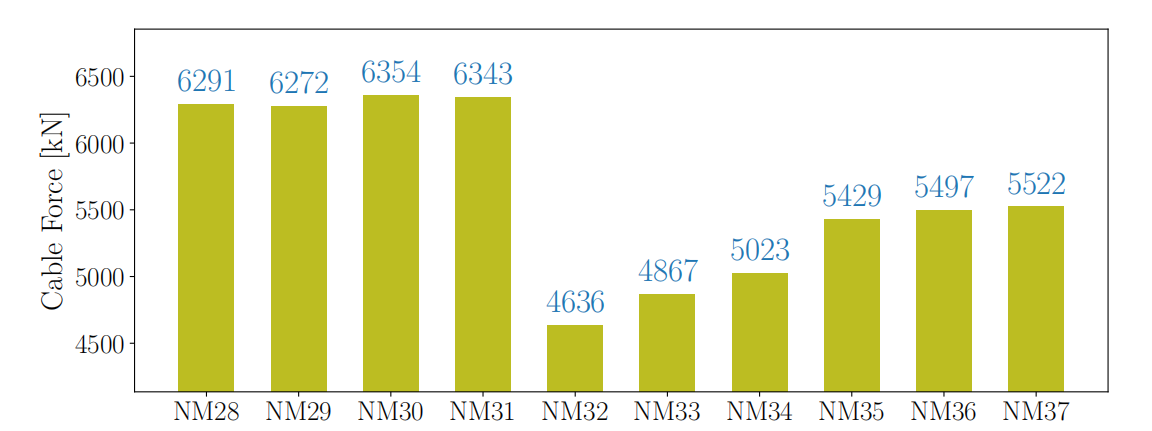
 图11 NM28-NM37索在第一个工况下的索力

3.4 全部工况数据汇总

用相同的方法和流程可以计算NM28-NM37索在所有37个工况下的索力。结果汇总如图12所示。

由图可知，本文提出的算法可以准确求出所有370个索力。且该方法全程无需人工干预，极大地提升了数据处理的速度与准确度。

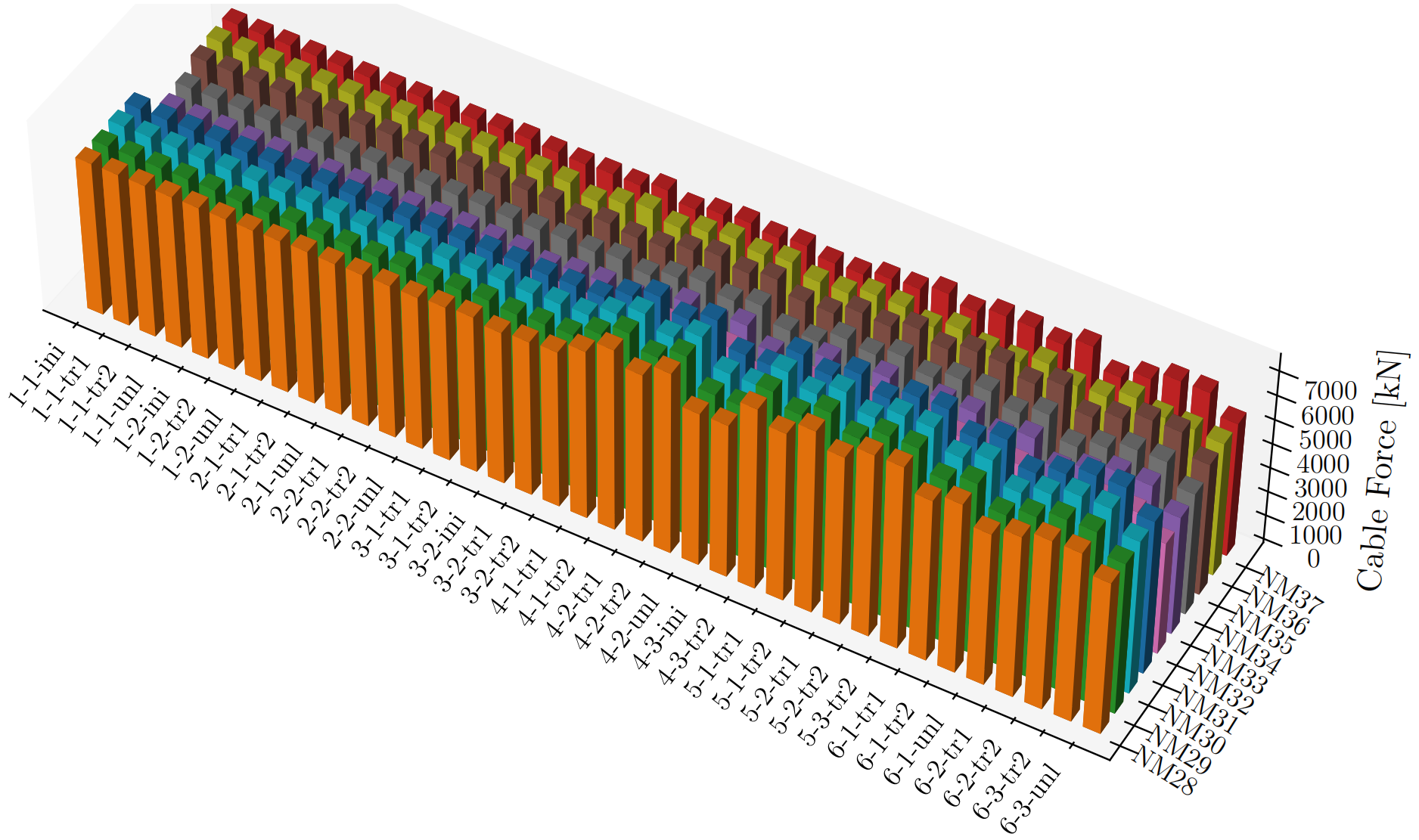
 图 12 NM28-NM37索在所有工况下的索力汇总

3.5 微波雷达与加速度计的试验结果比较

此外，本研究还对加速度计和微波雷达的测量结果进行了比较。结果表明后者的精度更高；而前者容易受环境噪声的干扰，可能会产生较大的拾峰误差（图13）。

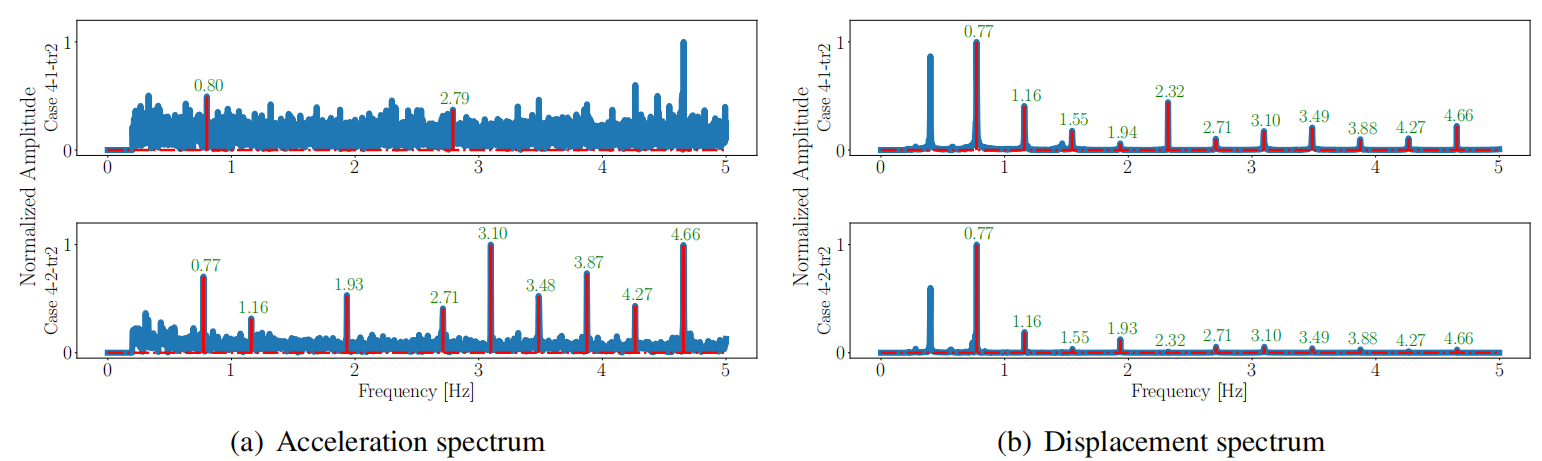
 图13 加速度计和微波雷达的频谱比较

4. 结论

本文提出了两种算法以实现基于微波雷达的全自动非接触式索力识别方法。该方法实现了对斜拉桥中大量斜拉索在不同荷载条件下的全自动索力识别。在鳊鱼州大桥上进行的现场试验验证了该方法的可行性和高效性。具体结论如下。

（1）所提出的快速筛峰算法FSM可以从位移的频谱中自动提取拉索的各阶特征频率，该算法具有线性时间复杂性。

（2）所提出的加权哈希投票算法WHV能够对FSM识别所得的模态频率加以定阶。

（3）本研究发现，相比于传统的加速度计，用微波雷达进行索力识别更加稳定与精确。这可能是因为加速度计只能安装在靠近梁体的位置，因此易受拉索边界条件的影响。

5. 参考文献

[1] Y. Fujino, Vibration, control and monitoring of long-span bridges—recent research, developments and practice in japan, J. Const. Steel Res. 58 (1) (2002) 71–97.

 [2] L. Sun, L. Chen, H. Huang, Stay cable vibration mitigation: A review, Adv. Struct. Eng. 25 (6) (2022) 3368–3404.

 [3] B. Peeters, G. Couvreur, O. Razinkov, C. K¨undig, H. Van Der Auweraer, G. De Roeck, Continuous monitoring of the øresund bridge: system and data analysis, Struct. Infrastruct. Eng. 5 (5) (2009) 395–405.

 [4] A. B. Mehrabi, In-service evaluation of cable-stayed bridges, overview of available methods and findings, J. Bridge Eng. 11 (6) (2006) 716–724.

（更多详细内容可参考实际文章）