1. 为什么集成？

“三个臭皮匠，顶个诸葛亮”、“众人拾柴火焰高”、“兄弟齐心，其利断金”——种种耳熟能详的谚语指向一个古老而深刻的道理：良好的合作关系总能带来更好的结果。对于机器学习亦然——如果一种机器学习模型在问题的某一方面展现出良好的性能，另一种机器学习模型在问题的另一方面也展现出良好的性能，那么用一种良好的方法把这些模型结合起来，就能够得到在问题所有方面都表现优异的预测模型。

集成学习，是一种集成多个机器学习模型的预测结果并给出最终预测的算法。集成学习的根本思想就是集成各基学习器的优势减少预测误差——这里的误差既可以是Bias（即模型预测能力差），也可以是Variance（即模型泛化能力差）。通常来说，选择一种好的集成方法至少可以降低一种误差，如Bagging算法擅长提高模型的泛化能力，而Boosting算法擅长提高模型的预测能力。当然，作为一名优秀的机器学习（炼丹）工程师，妙手偶得一种既能提高泛化能力，又能提高预测能力的算法也不无可能。

2. 怎么集成

2.1简单集成算法

谈及模型集成，最简单而直接的方法就是将各个模型的输出做简单平均Unweighted average（对于回归问题），或按照各模型的结果投票Majority voting（对于分类问题）。

简单平均的集成结果是各个基模型的平均。这种做法的好处是简单明了，且各个基模型性能相似是往往能够取得较好的结果。但是它的坏处是：由于平均过程未加权，因此集成结果受那些性能较差的基模型结果的影响大。因此，简单平均不适用于存在某些效果较差的基模型的集成场景。简单平均适用于回归问题。同时对于基模型能够输出各类别概率（如朴素贝叶斯）的分类问题，简单平均也能适用。

投票是根据基模型的分类结果投票决定最终的分类结果。对于异质模型Heterogeneous Models（即根据不同算法建立的模型，或网络结构不同的模型），多个异质模型在同一个问题上犯错的可能很小，因此可以通过投票获得更加准确的分类结果。从某种角度看，投票之于分类问题也是一种加权的简单平均方法。

集成算法可以加权，如上文提到的简单平均和投票，也可以加权。加权的继承算法和加权的算法相比，唯一的区别就是对各基模型的结果按照预先给定的权重集成。权重是由一个顶层学习器根据数据训练得到的集成算法也是后文将要介绍的Stacking。

2.2 Bagging

 Bagging看上去是一个词，实际上是Bootstrap Aggregating的缩写。Bagging算法的基本思想是对训练数据进行n次抽样，每次抽样得到的数据用来训练一个基模型学习器，最后再将基模型的结果集成得到最终预测结果。

 Bagging算法的设计主要为了提升模型的泛化能力（即降低Variance）。在训练基学习器时，Bagging算法通过随机采样将训练集分割为数个子数据集输入到基学习器进行训练——此时各个基学习器用于训练的数据少了，因此各个基学习器训练效果差了；但是不同基学习器用于训练的数据的分布不完全相同，因此多个基学习器的集成将提升模型总体对不同分布数据的预测效果。

 Bagging算法采用的基学习器通常来自同一类——如随机森林算法实际上就是对决策树算法的Bagging。

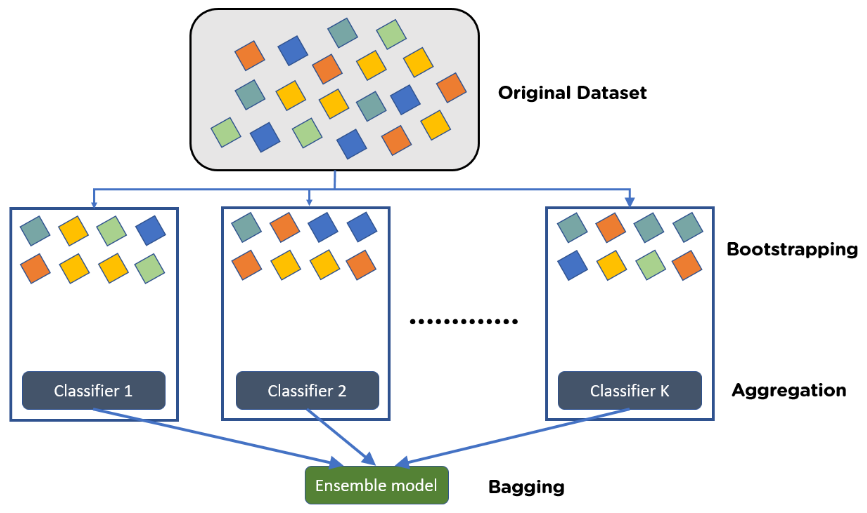
图1 Bagging分类算法示意图

2.3 Boosting

 Boosting算法的基本思想是不断提高错误预测样本的权重，以收获更加精确的预测效果。因此和Bagging并行式的基模型训练不同，Boosting对于模型的训练是串行的。

 Boosting的提出是为了提高模型的预测能力（即降低Bias）。在训练基学习器时，Boosting首先在一个基学习器上训练一次数据，然后根据弱学习器的预测对数据集进行权重更新，增加错误预测数据的权重同时减小正确预测数据的权重，然后在权重更新后的数据集上训练下一个基学习器。上述过程在Boosting的训练过程中会重复数次，直到得到n个排列好的基学习器。最后，Boosting可以通过加权平均或投票、提升树两种算法中的任意一种将各基学习器的结果组合起来，得到最终的预测结果。

 Boosting和Bagging一样，采用的基学习器通常都来自同一类。常用的Boosting算法包括AdaBoost (Adaptive Boosting)和基于GBDT (Gradient Boosting Decision Tree)的算法如XGBoost, LightGBM, CatBoost等等。

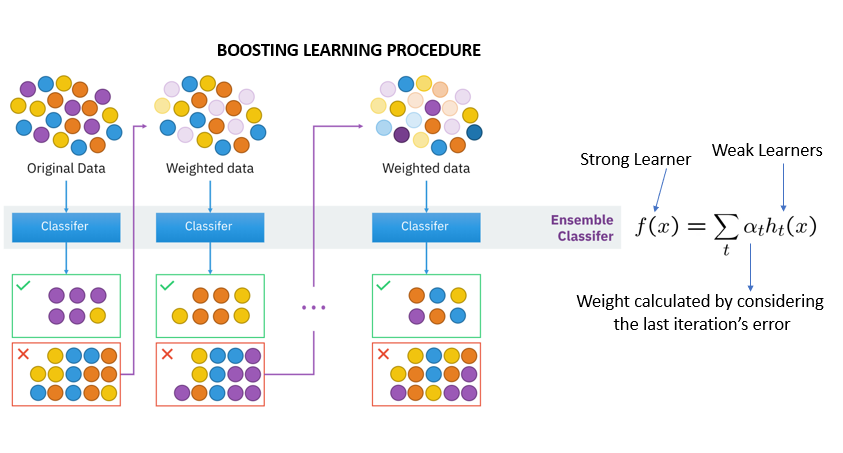
图2 Boosting分类算法示意图

 1.4 Stacking

 Stacking与Boosting和Bagging相比，恐怕是最简单粗暴的集成算法了。所谓Stacking（堆叠），即将多个机器学习模型堆起来，一层模型的输入是上层所有模型的输出（这种结构与神经网络具有高度的相似性）。每一层模型的训练与Bagging相同，都是并行开展的。只不过对于每一层的各个基学习器来说，其训练数据都是总体数据，没有经过随机抽样。

 Stacking算法采用的基模型是异质模型 (Heterogeneous)，异质模型的堆叠在增加总体模型的泛化能力的同时，也能提升模型的预测能力。但Stacking算法采用的基模型和Bagging相比是“强学习器”，再加上一层中基模型训练使用了总体数据，因此Stacking在训练过程中很容易发生过拟合现象。这就要求我们在训练基学习器时采用k折交叉验证的训练方法。同时过拟合现象与Stacking的层数相关，因此一般来说Stacking只采用两层模型。

 Stacking“提升模型泛化能力”和“容易过拟合”两个特征似乎有些冲突。但实际上Variance和Bias并不是独立的两个变量。Bias的下降（即预测能力的提升）通常伴随着Variance的上升（即泛化能力的下降）。Stacking对基模型预测能力的提升大于对泛化能力的提升，因此宏观上表现为Stacking的泛化能力下降了，容易发生过拟合。

 Stacking算法的关键在于基模型的选择和顶层模型的选择。基模型之间越异质化，总模型的泛化能力越强；基模型预测精度越高，总模型预测能力越强。同时顶层模型通常不建议选择太复杂的模型（也是出于泛化能力的考虑）。对于回归问题，简单的线性回归器也能发挥不错的效果。而采用线性回归器作为顶层回归器也等价于简单集成算法中的加权集成，只不过权重是由顶层回归器学习得到。

图3 Stacking回归算法示意图

3 参考

[1] https://www.simplilearn.com/tutorials/machine-learning-tutorial/bagging-in-machine-learning

[2] https://www.pluralsight.com/guides/ensemble-methods:-bagging-versus-boosting

[3] https://data-science-blog.com/blog/2017/12/03/ensemble-learning/